// ABSTRACT
This research explores methods of 3d printing vaults and domes using clay as a material, based on a study of precedents and traditional construction techniques. These structures require a high level of precision in their execution, which means they have a lot of potential in the field of additive manufacturing. On the other hand, it also presents a number of limitations related to the behavior of the extruded material during and after the printing process.
Based on an understanding of vaults and domes in masonry construction, their geometric constraints, building processes and their evolution through history, we aim to develop a set of parameters to adapt those techniques to 3d printing. Our goal is to achieve geometries that can be printed without extra supports or formworks, in order to reduce cost, time and waste of materials.
In order to achieve that, we investigate how to optimize the geometries, the robotic setup for printing and the strategic use of infills. We explore the scale of the brick, the layer and the finished geometry, in an attempt to broaden the possibilities of printable geometries that we know today.
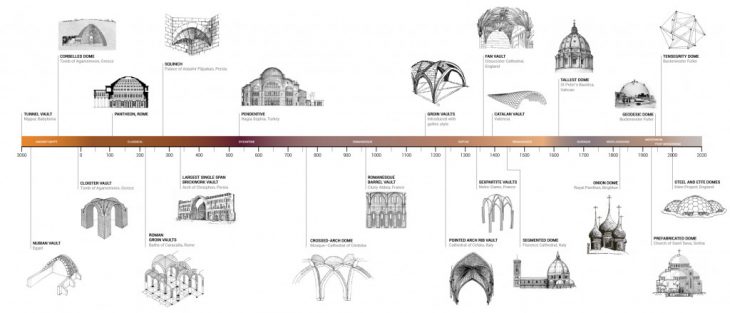
// HISTORICAL TIMELINE
We study a timeline of vaults and domes dating back to 3.000 B.C, when they consisted in simple structures composed by layers of bricks. With the introduction of new structural elements they start taking different geometries and compositions.
// PART I – DOMES
To start out the research we wanted to understand the complications that come with 3d printing domes with clay by printing very simple geometries. The results from these first prints helped us understand how different types of curves result in different levels of stability.

GEOMETRIES
For the next tests, we chose to define a base geometry inspired by the dome of Santa Maria del Fiore, in Florence. It’s historical importance and the fact that it was built without any centring is something we want to translate into our research in 3d printing. So we define a base geometry that consists in a segmental catenary dome.

The local inertia was analyzed and later tied into the results that we had from the test prints. The lines that devide the segments, being here responsible for the overall stiffness of the printed volume, are desired to show higher local inertia values.

TEST PRINTS
16 out of the 28 geometries were printed, showing various levels of stability and buckling. The geometries with good distribution of their local inertia tended to buckle a lot or not even finish printing, due to the lack of stability along their lines of force. The best results were observed on the geometries that had defined lines of force with high inertia, along the lines that define the segmental half dome.

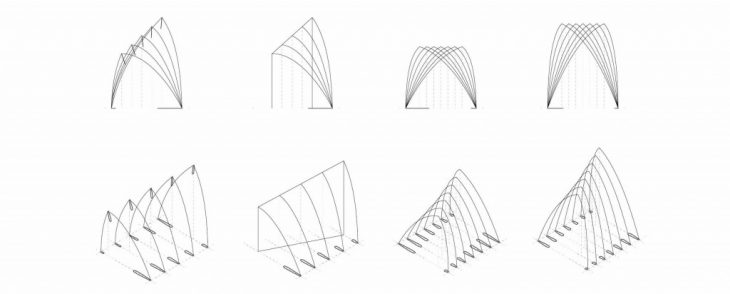
// PART II – BARREL VAULTS
The first geometries explored were simple barrel vaults structured by arches. Four different variables were defined for the test prints, in order to understand how to deal with the cantilever, the ratio between height and span, the printable lengths, and the benefits of using support walls. All of the geometries were printed and, from these tests, we were able to extract a set of parameters that can be applied to more complex geometries. The variables analyzed were the thickness of the arch, the type and height of the curve, the use of supports and the span.

To understand why some prints fail, we needed to analyze the deviation of the center of gravity during the print, layer by layer. To ensure that the vault can be printed, it’s necessary to look at the cantilevered sections before they are joined at the top and become a full arch. If the center of gravity doesn’t exit the support area, the print is likely to be successful. The base geometry has a span of 150mm.
TEST 01 – Arch thickness
For the first test, we experimented with the thickness of the arch, using a simple vault based on a catenary curve as a starting point. The thicknesses tested were 20, 25 and 30mm.

TEST 02 – Curve type/height
On the second test, two different variables were explored. First, using the same catenary curve, we varied its height. Then, we picked the best option from this test and applied variable cross sections on the top of the arch, to observe if this affected the center of gravity deviation.

TEST 03 – Semicircular curve
When experimenting with semicircular vaults, we encountered a problem unrelated to the center of gravity. These vaults have very slight cantilevers due to their reduced height, but when scaled up, the bridge between the two legs becomes too wide. For this reason, we experimented with three different scales of semicircular vaults.

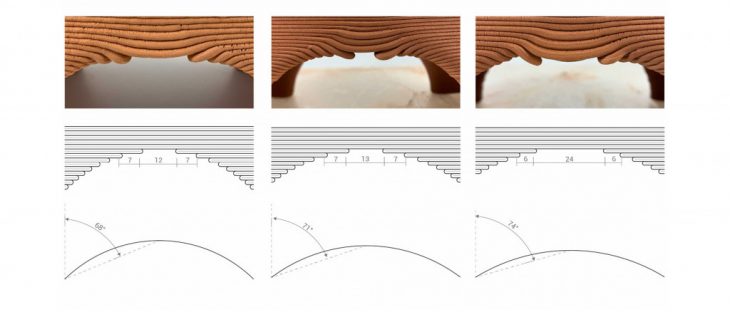
TEST 04 – Span
This test played with the distance between arches, without any other elements or modifications to the walls, in order to define the maximum printable span that doesn’t result in buckling under these conditions.

// PARAMETERS
Layer scale
Based on the experiments with different types of curves, slicing distances, heights and thicknesses, we conclude with some basic parameters to ensure a print with stable cantilevers/overhangs.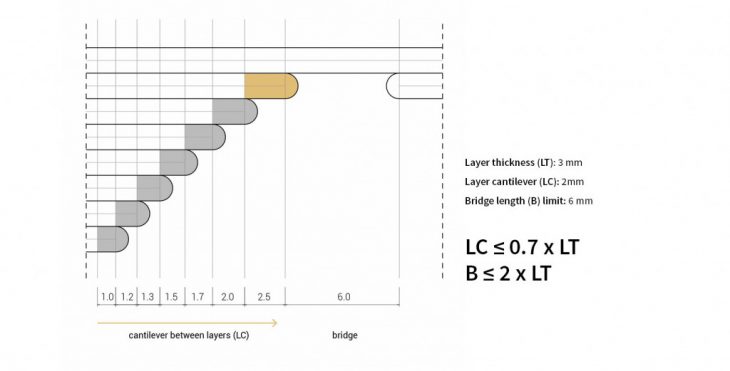
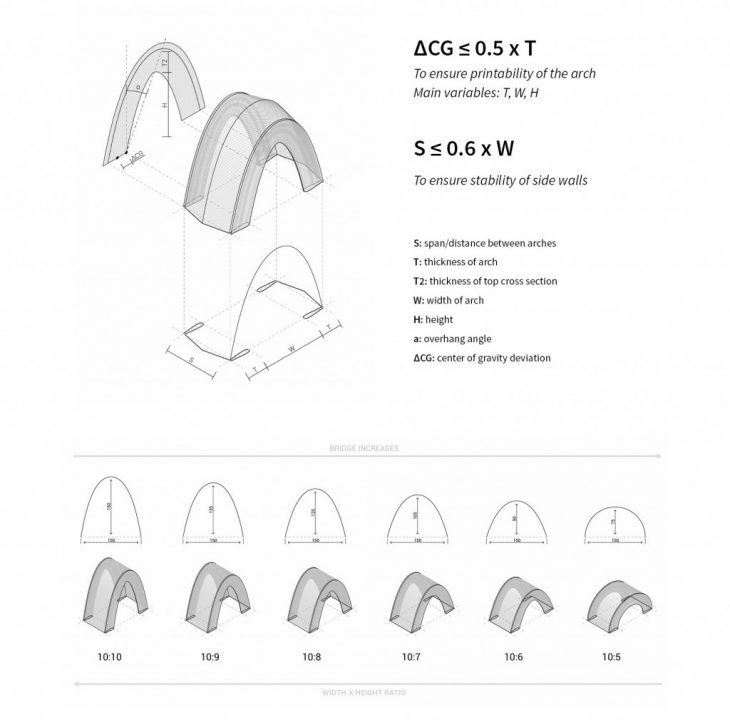
Overall geometry of basic barrel vaults
We also summed up some basic geometric proportions applied to barrel vault structures defined by arches. These proportions should allow us to complexify the shapes further on.
// PART III – RIBS

After succeeding to define a set of basic parameters to print a basic vault, we still needed to find a solution to close its top. Our strategy was a reinterpretation of the concept of ribs used in the Gothic period in order to connect the geometry at the top and print on top of it, completely closing the roof.
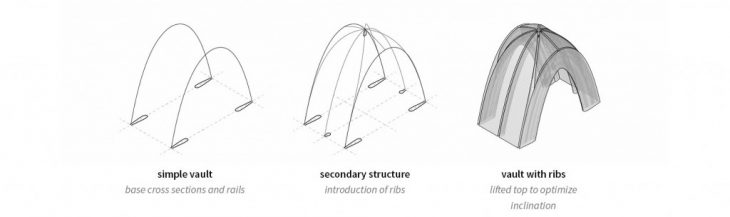
Adding this secondary structure provides a triangulation and reduction of the span per printed layer. When the ribs touch towards the top of the vault they create a base surface for the last layers to be printed on top of.
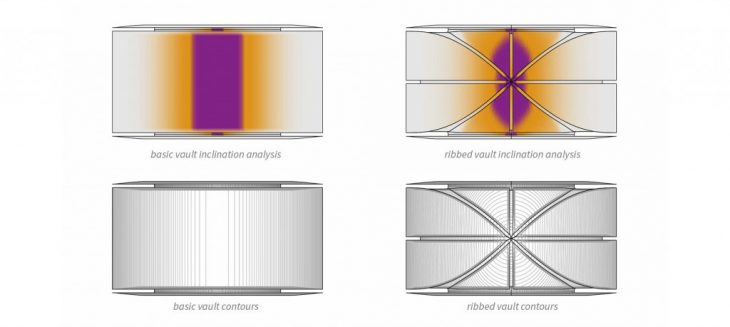
PARAMETERS
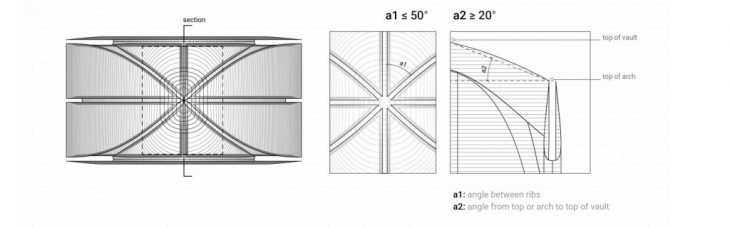
RIBBED GROINED VAULT

APPLICATIONS
To conclude, we analyze the potential application and limitations of the base geometries explored in our research.
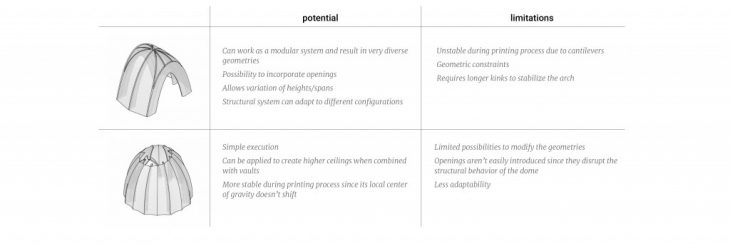
// PROTOTYPE
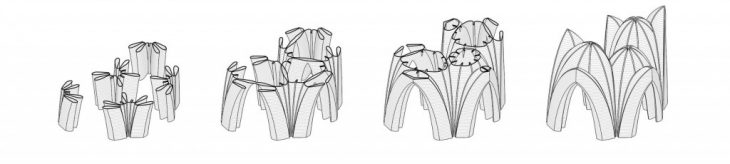
On our prototype we wanted to demonstrate how this system can be modified and take different configurations by deforming, scaling and connecting arches. Starting from 2D studies, we reach a final geometry consisting of five main arches of different heights and spans, connected by secondary arches that are then joined by ribs.
The area occupied by the support points is minimized, while the covered area is maximized. The interior spaces have different ceiling heights and degrees of openness.

Plan and section
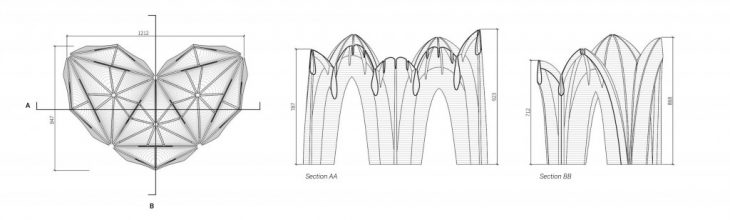
Production
Printing in the larger scale brought a new set of challenges, with the limitations brought by the weight and the behaviour of the material during printing and drying. It brought the necessity of dividing the printing sessions and adding some time for drying before continuing the print. The prototype was printed in three days, using a total of 355 kg of clay.


</p>
3D printing vaults and domes is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in Open Thesis Fabrication 2020/21 by Students: Brenda Freitas and Nitha Shivapuram, Faculty: Edouard Cabay, Alexandre Dubor, Kunaljit Chadha, Ashkan Foroughi Dehnavi
