Objective
With AI and machine learning invading the AEC industry, we are offered an opportunity to improve the performance of our existing tools. If trained well, the model can generate a prediction faster than results generated with a simulator.
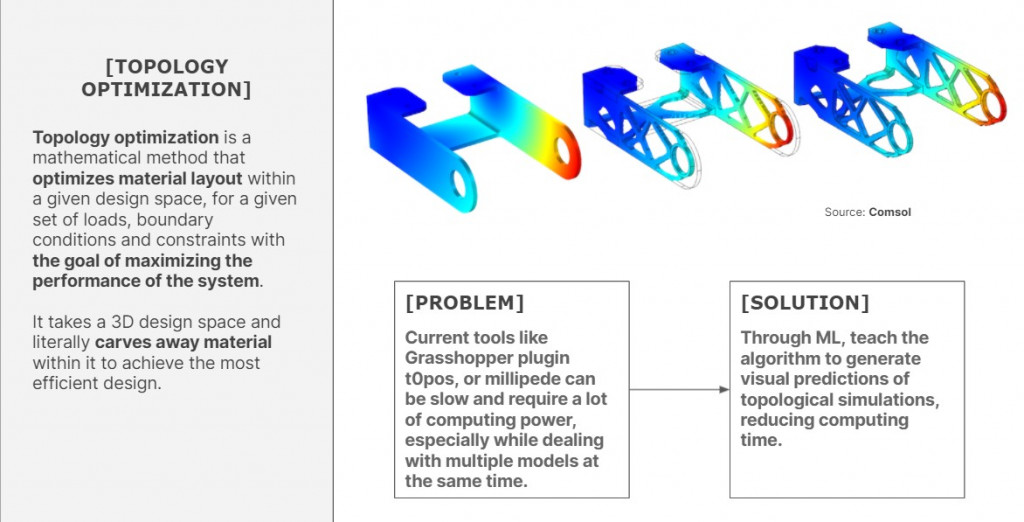
From previous experience, topology optimization tools like a Grasshopper 3D plugin t0pos or millipede can take a long time to compute geometries. We found 3D Convolutional Neural Networks (3DCNNs) to be an applicable solution. We looked at the 3D MNIST dataset of 3D handwritten numbers as a reference. The objective of this research is to apply machine learning methods to generate a visual prediction of the topology-optimized geometry given the loads, support, and a volumetric bounding box.
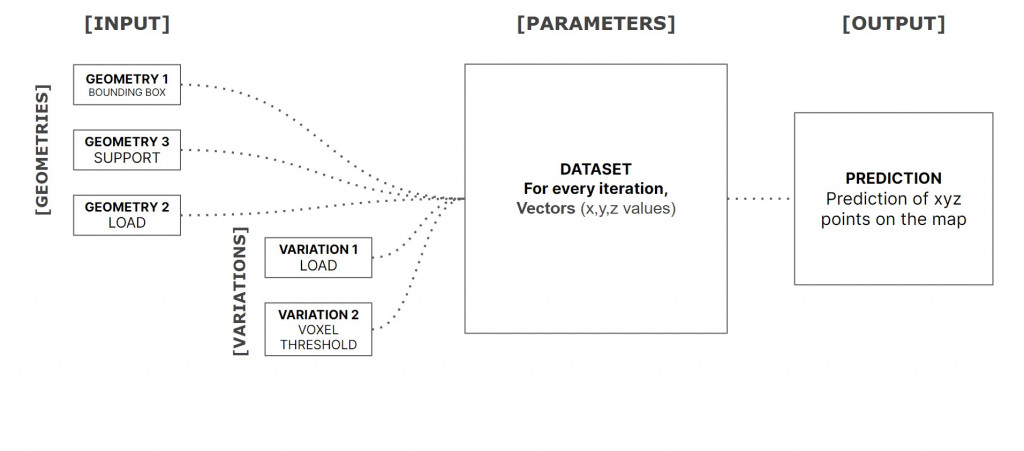
Dataset
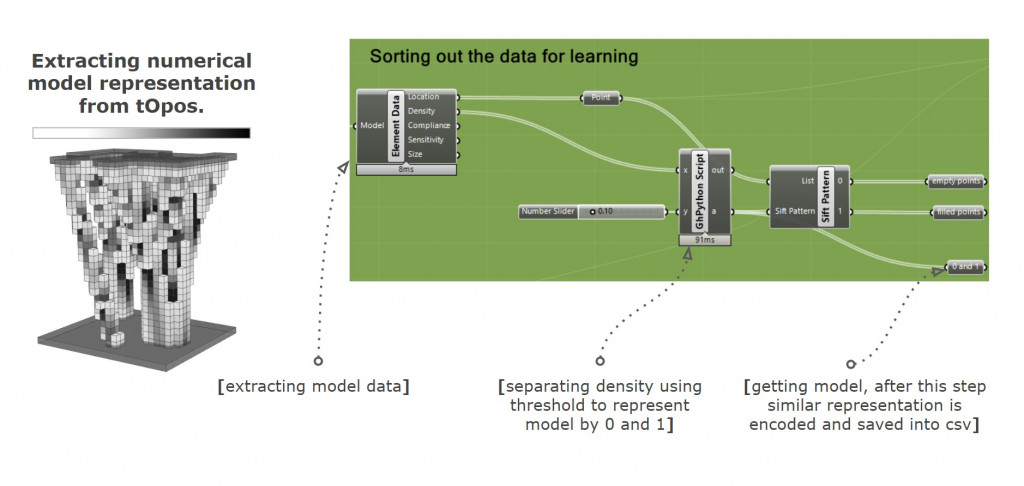
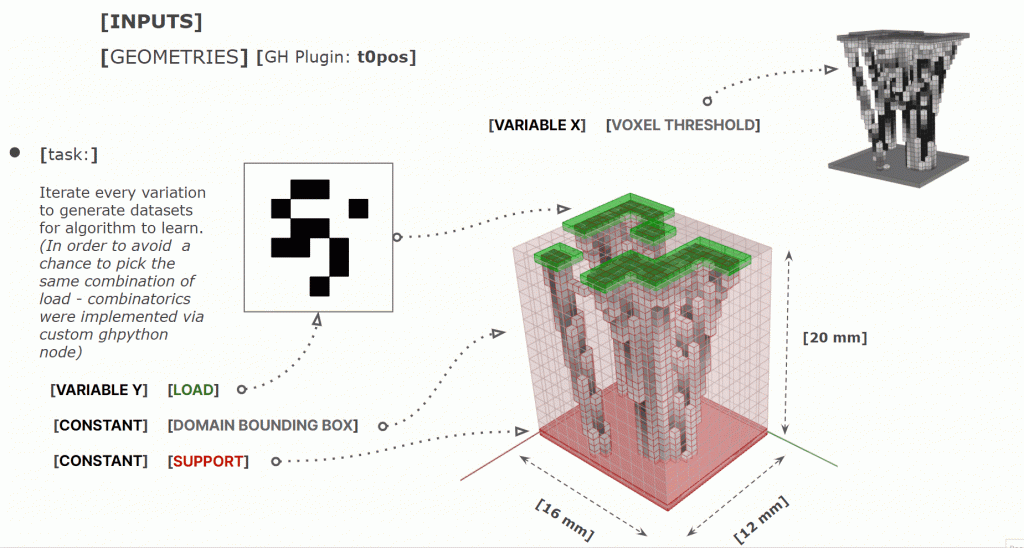
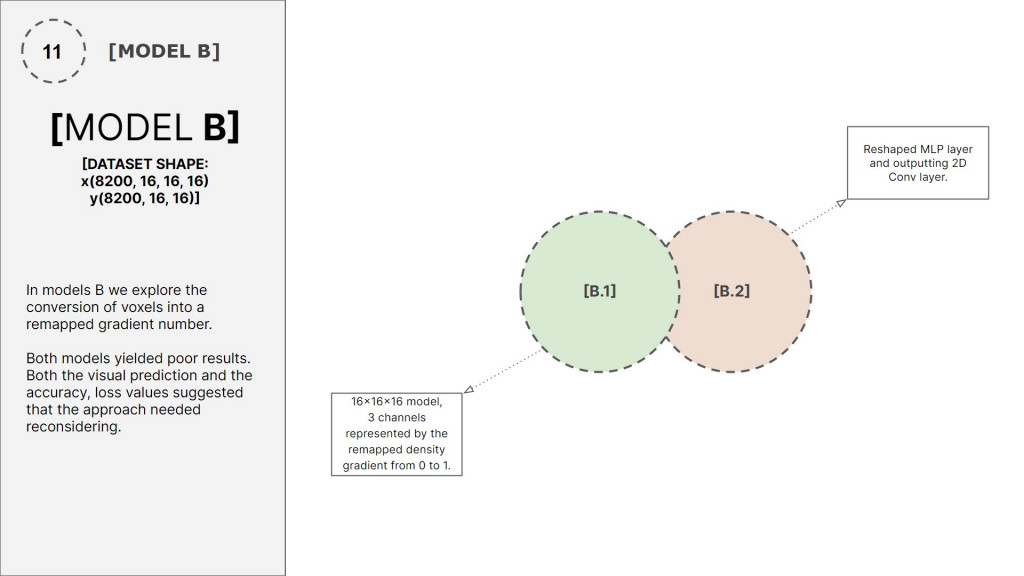
The initial challenge was dataset preparation in grasshopper. We used t0pos with a fixed scale support and bounding box, while iterating the top layer (loads). We prepared two datasets: a less complex binary dataset that only recognizes if there is a voxel or not, and a more elaborate data with a gradient that maps the density of voxels.
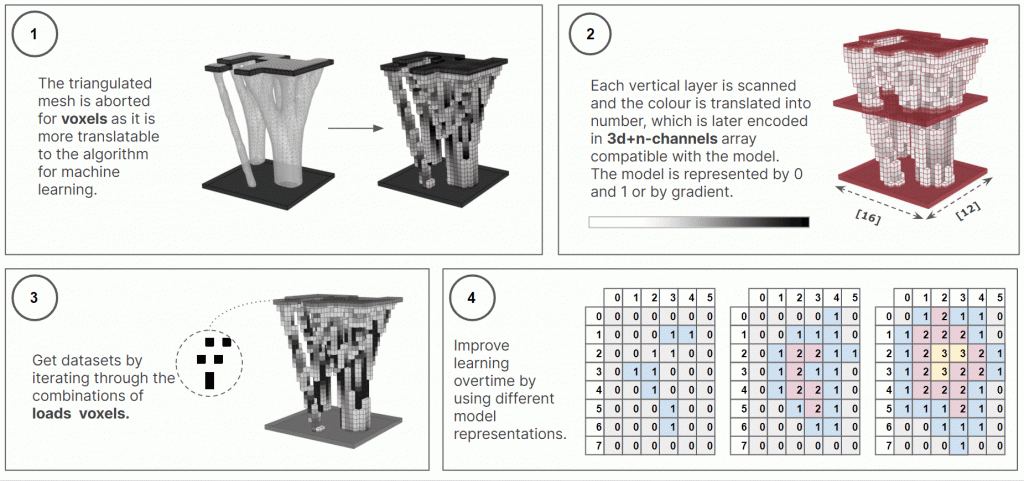
[CNN Kernel]
[Load Iteration]
Machine learning
As mentioned earlier, we looked at 3D Convolutional Neural Networks to develop computer vision and have the algorithm decipher our input geometries.
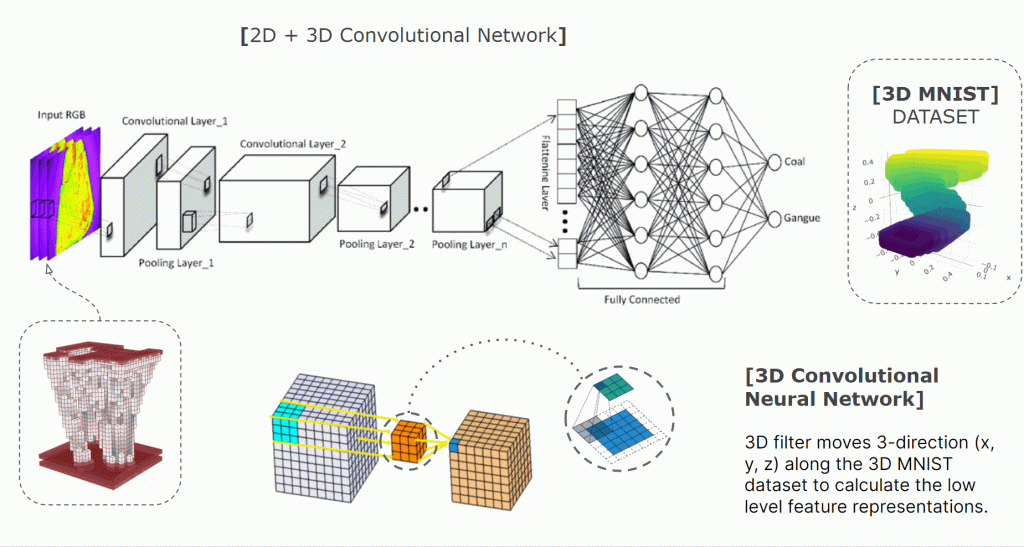

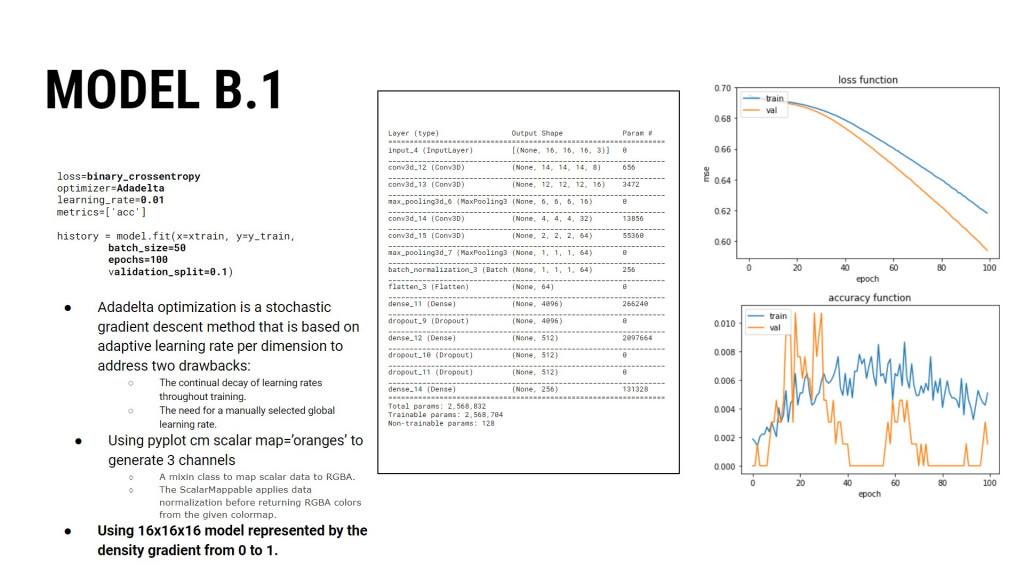
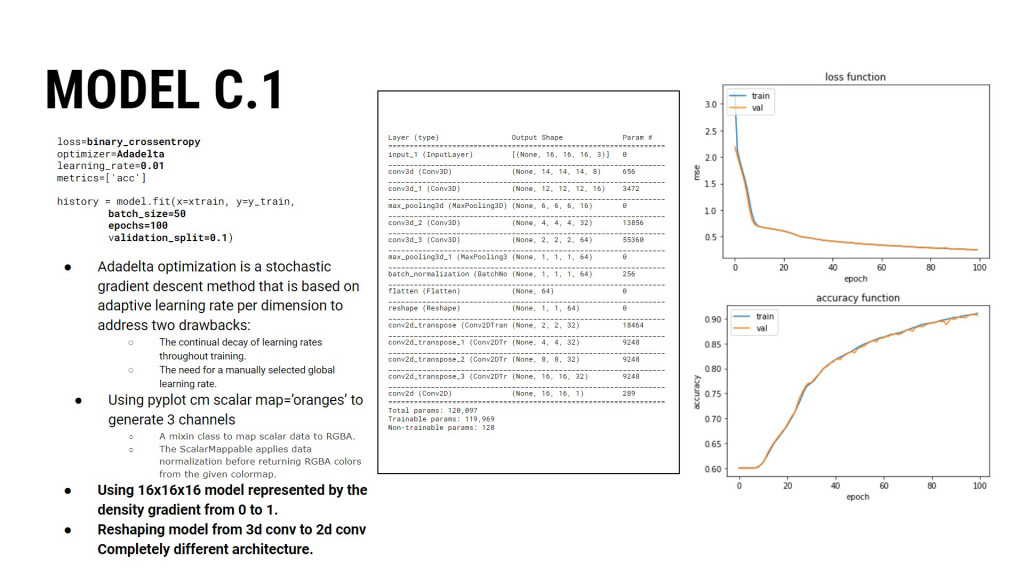
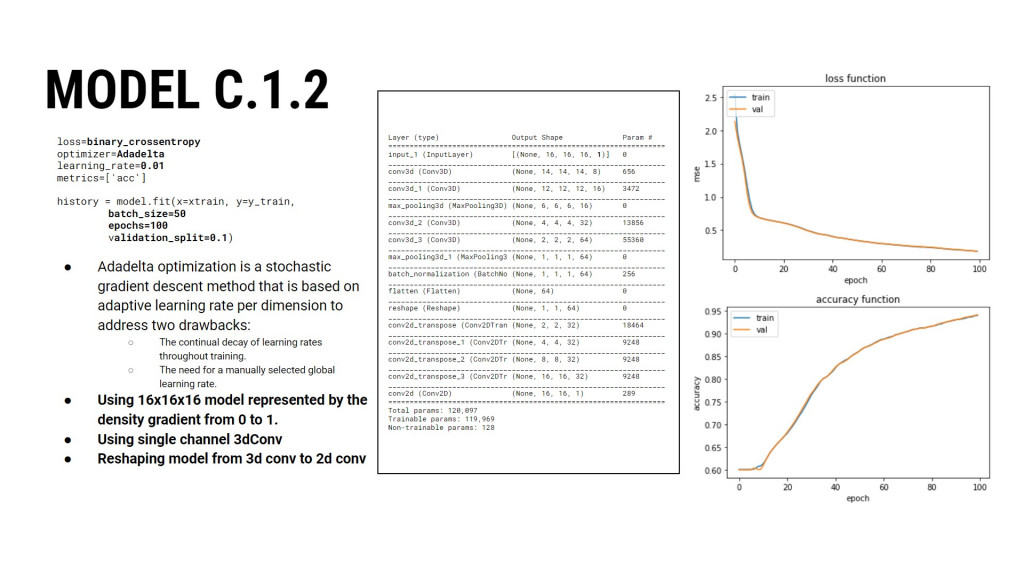
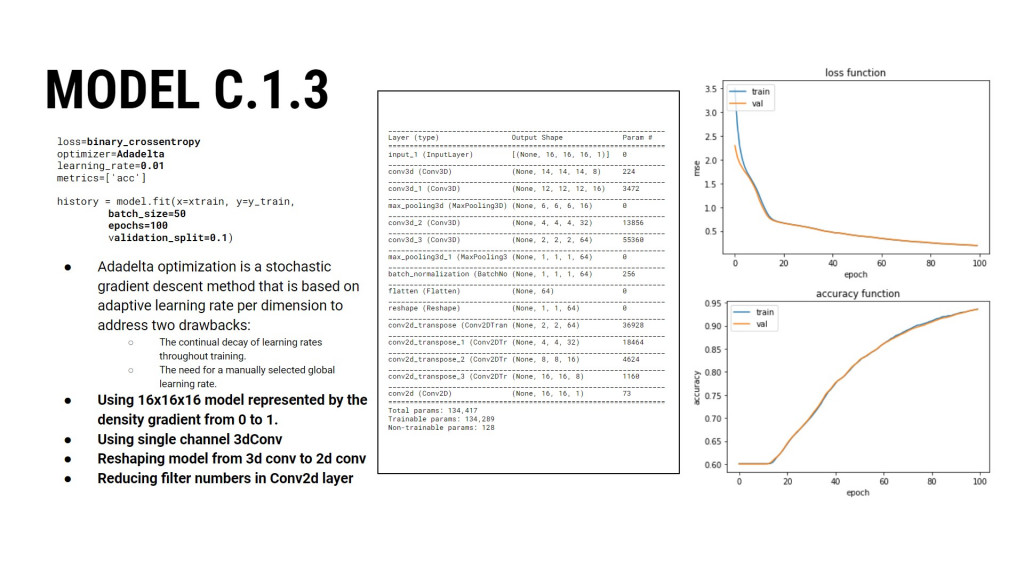
We randomly divided the dataset with a train split from Scikit-learn to have more validation data. While creating the model’s architecture, we both increased and decreased the number of MLP layers, switched between 1 and 3 channels, tweaked hyperparameters, optimizers, learning rate and tried completely different architectures.
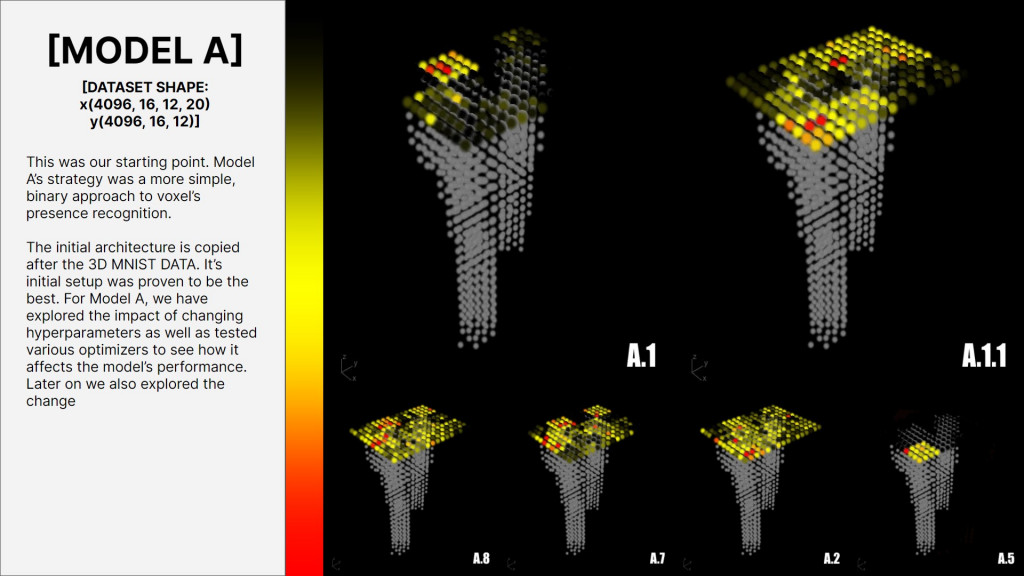
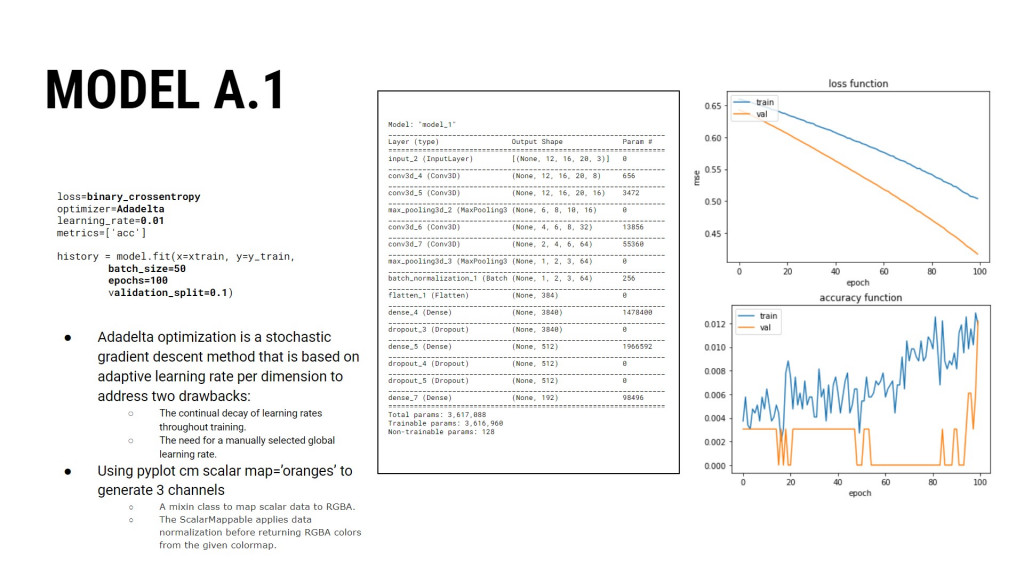
MODEL A

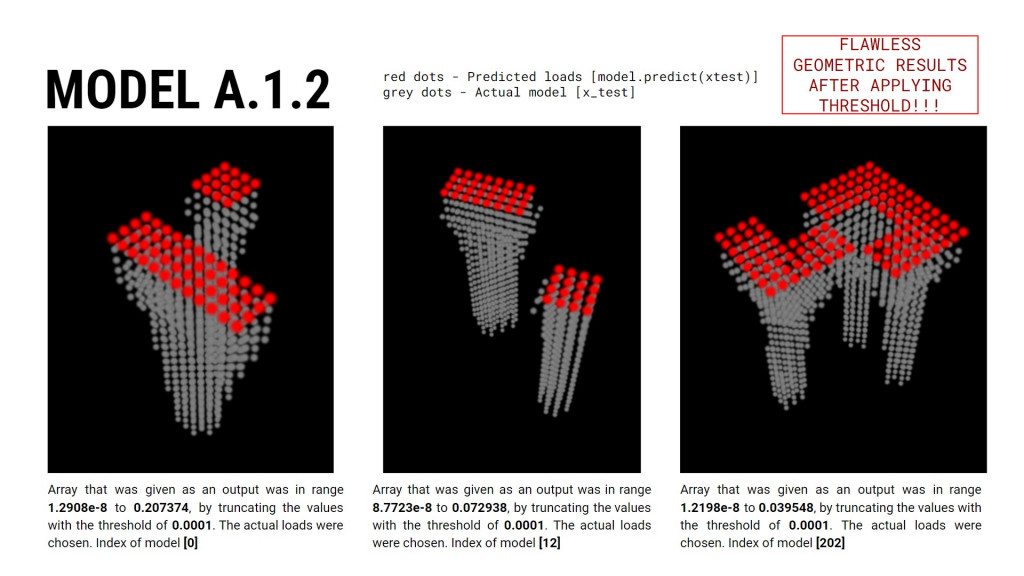
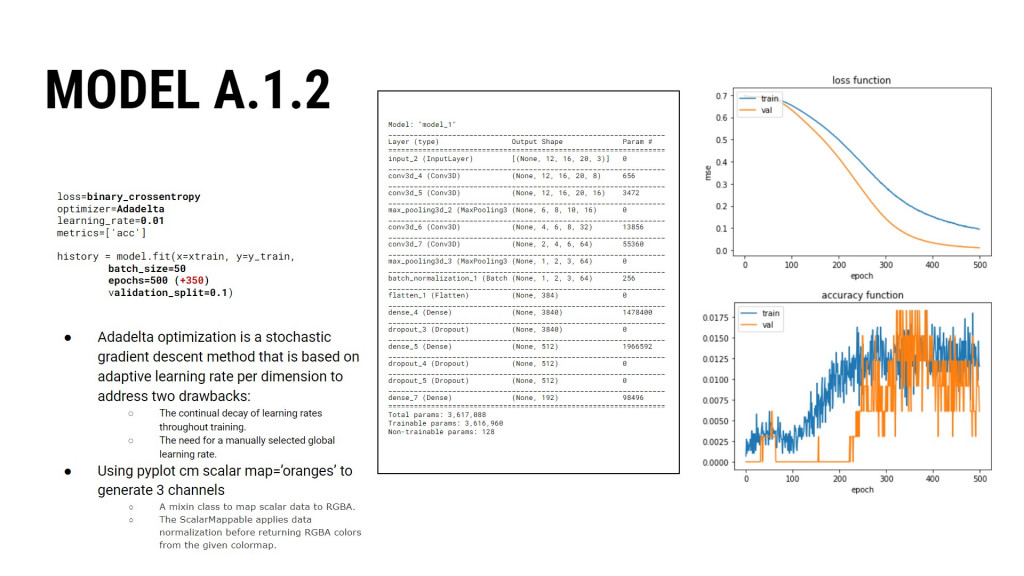
MODEL B


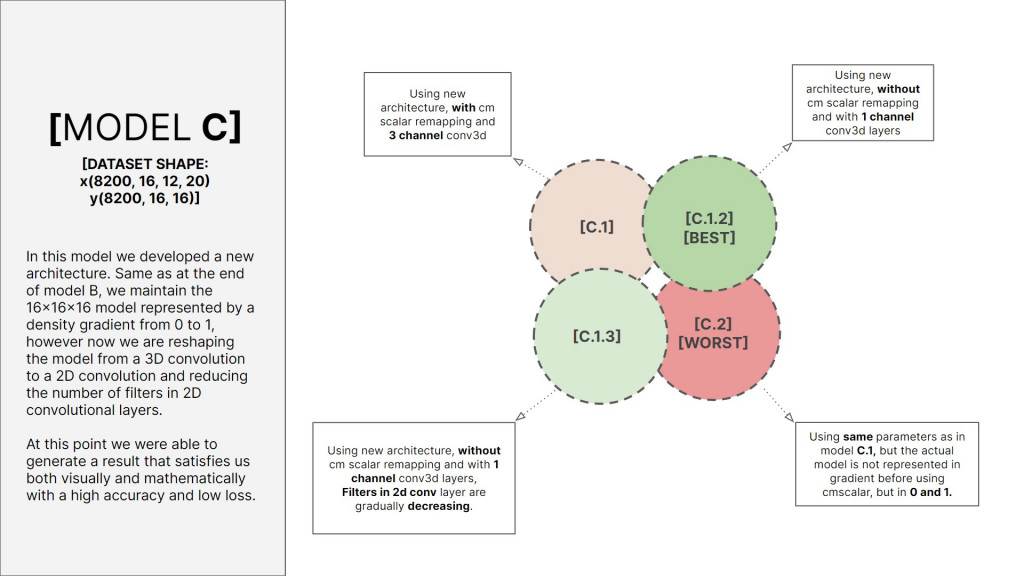
MODEL C


[New Architecture]



Conclusion
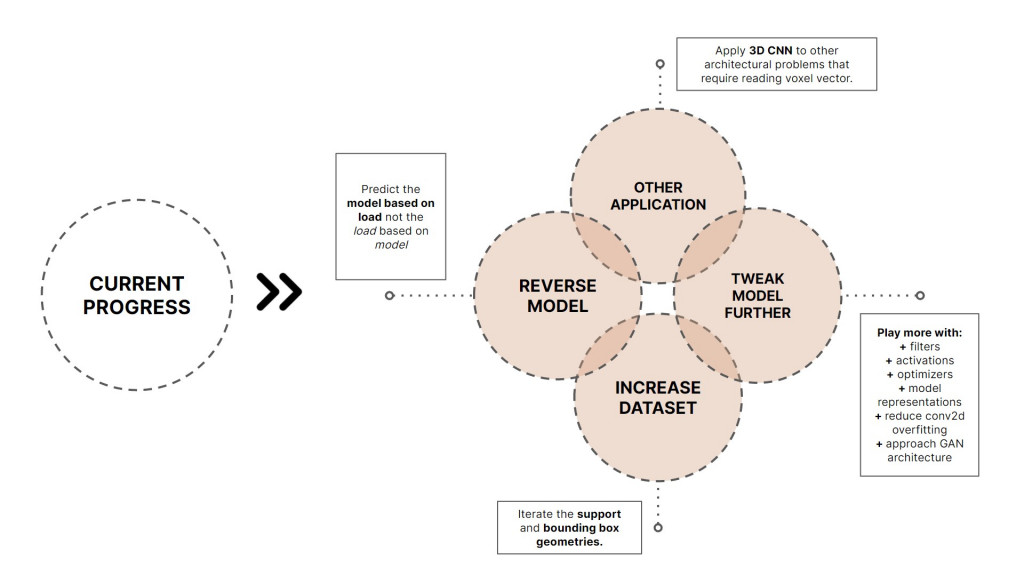
Given the time and reference constraint, at some point we had to shift focus to trying to predict the load as opposed to the geometry. There are many possibilities of moving forward: the first objective would be to reverse the model to learn to predict the vectors of voxels of the model as opposed to predicting the load. Further advancement includes expanding the dataset by beginning to iterate the support and bounding box geometries and refine hyperparameters for better performance. Above all, this research showed us a way to apply machine learning functions like 3D Convolutional Neural Networks in architectural contexts.
Credits:
Students:
Aleksander Mastalski, Andrei Okolokoulak
Faculty:
Gabriella Rossi, Iliana Papadopoulou