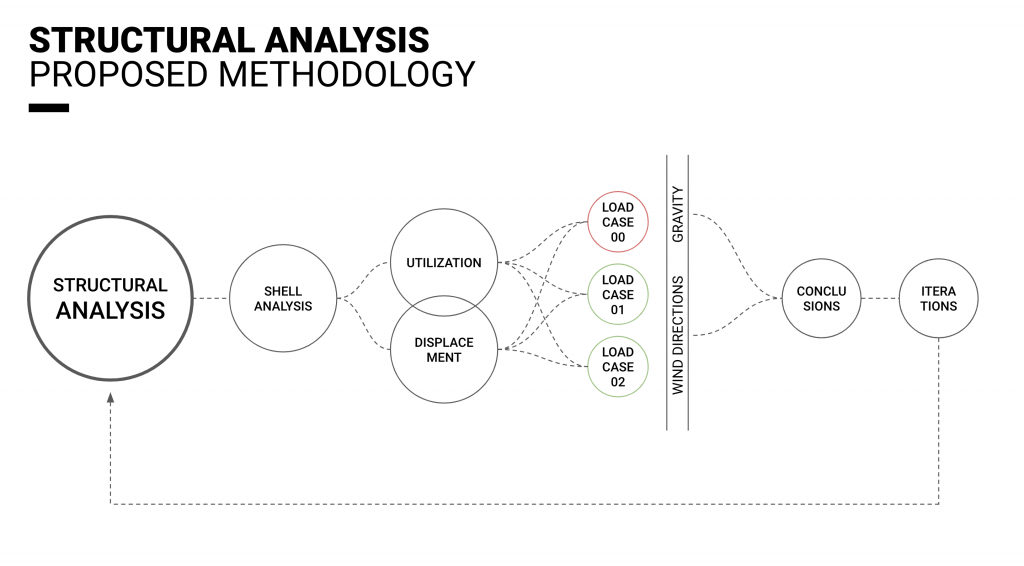
Structural Aspect of Folding Plywood Panels.
The objective of the project was to study a natural system and see how its logic is translatable into architecture. What started off as an observation of a specie of a palm tree, quickly escalated into a study of the folding in origami.
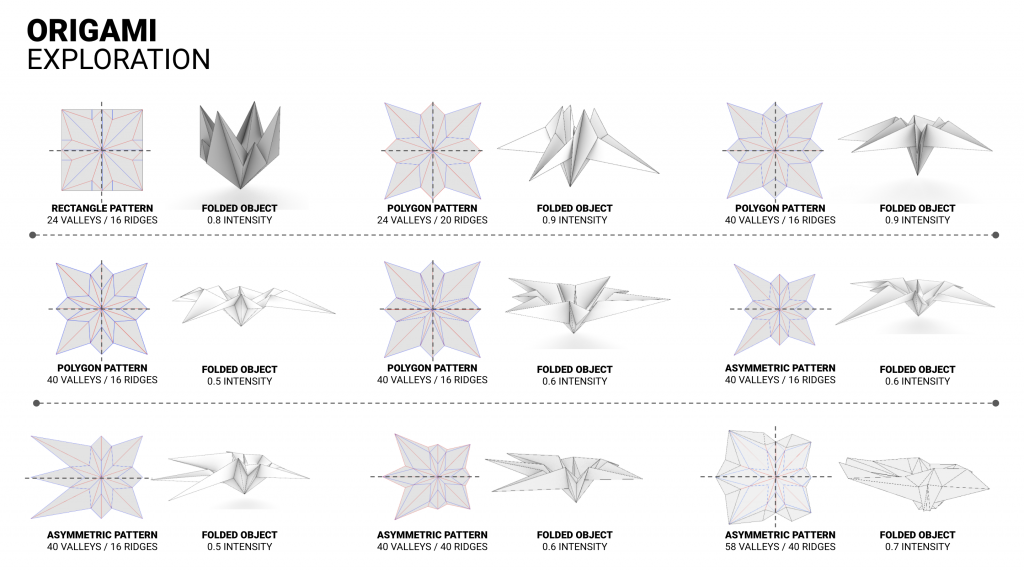
Our team has been working on different variations of a pavilion made out of plywood panels. The pavilion is a result of folding experimentation done in Kangaroo. For this project, we first tested different folding plans seen below to come up with a few geometry variations that we could later test in Karamba for structural analysis.
After reviewing the iterations, we chose three versions to structurally analyze to see how they compare and what we can learn. Our strategy was to use displacement and utilization values and visual representations to guide us through comparing the models and their structural behaviors.
The versions we chose gradually improve parameters such as symmetry and leg openness, to finally reach a desired result in version III.
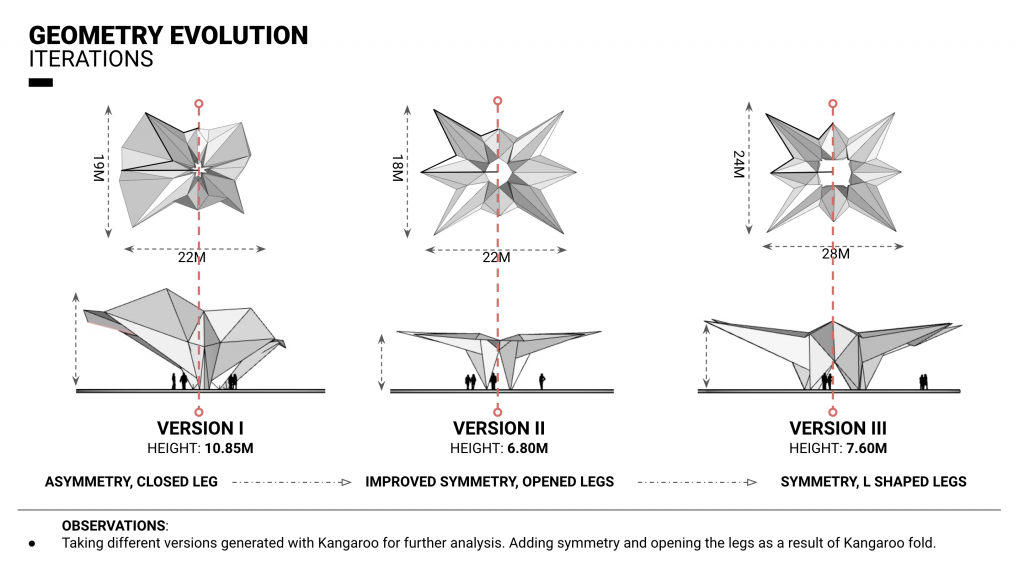
VERSION I: Asymmetrical, big single cantilever. One le
VERSION II: Improved symmetry, four legs with a sharp, singular support point.
VERSION III: Improved symmetry, leg improved to have a more stable “M” shape.
UTILIZATION ANALYSIS
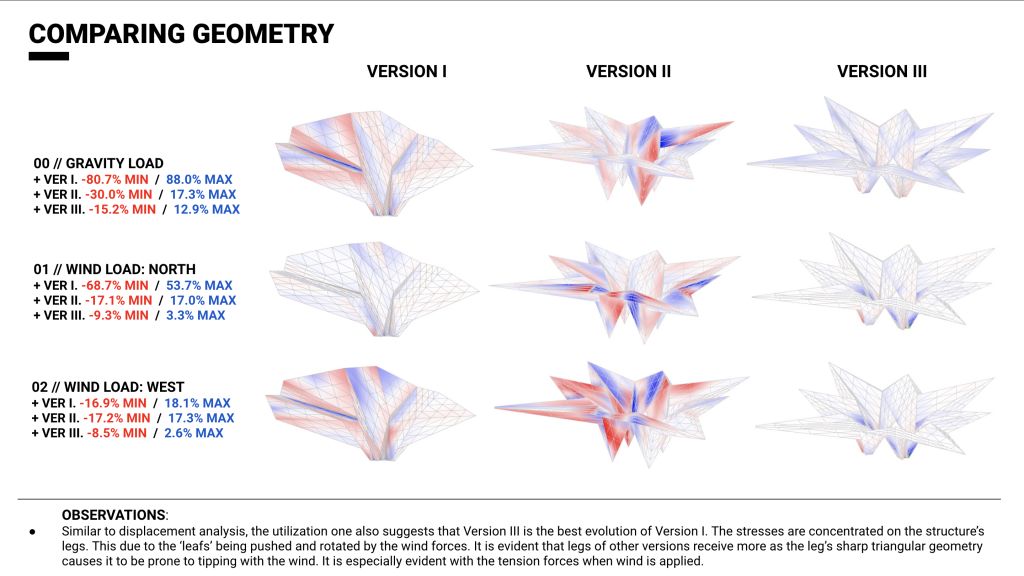
DISPLACEMENT ANALYSIS
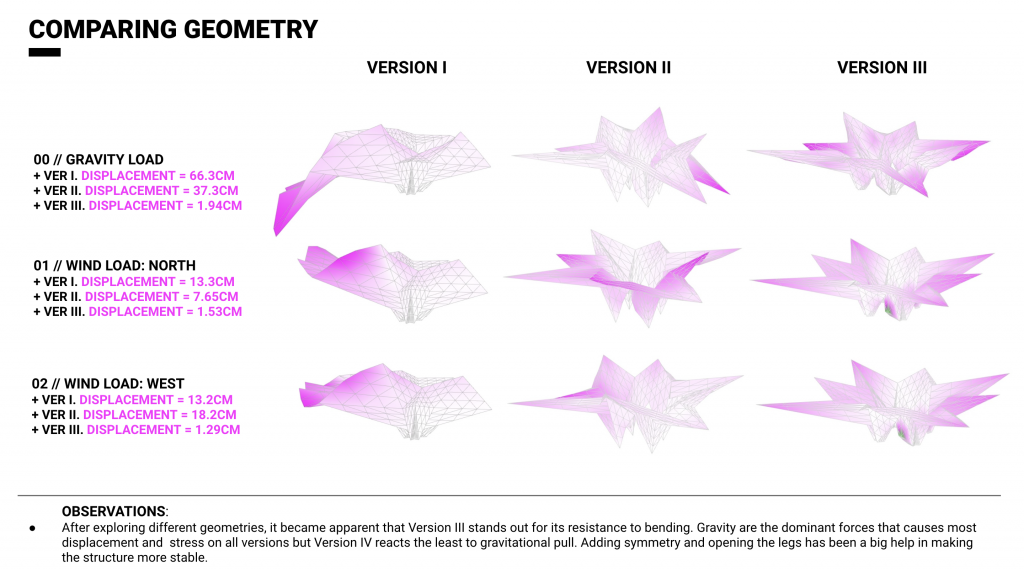
After analyzing the three versions it became apparent to us that working with a cantilever will be tricky. Not only does it want to fall down with gravity and self weight, but also its large area catches the wind and makes the structure want to rotate, which sends a lot of tension stress on the legs. It is evident that in all cases, the gravitational pull is the dominant force and it is noticeable that Version III is least impacted by gravitational load. It is noticeable that with gravity, the cantilevers are trying to make the structure unfold back into flat position. The analyses inform us that Version III is the most optimized geometry given that the utilization and displacement values drop with to very low figures.
We have concluded our geometry search with Version III. It is balanced and stable due to its “M” shaped legs. The broad cantilevers also assist in preventing the structure from tipping.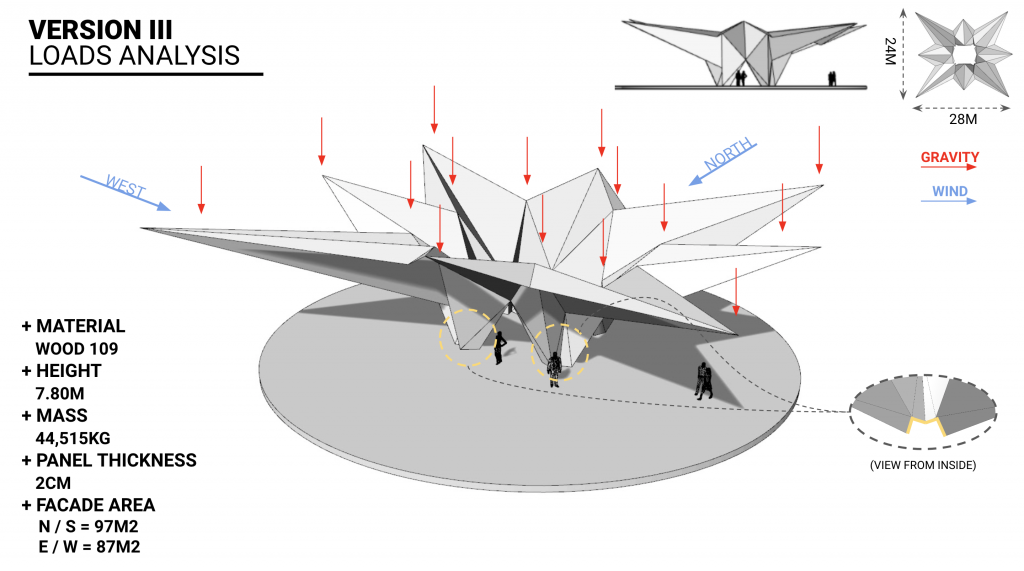
After we were content with our geometry, we looked for ways to further improve the stability and prevent the structure to want to unfold. We decided to test out two versions of implementing a tensioning cables that would further pull the structure together inwards.
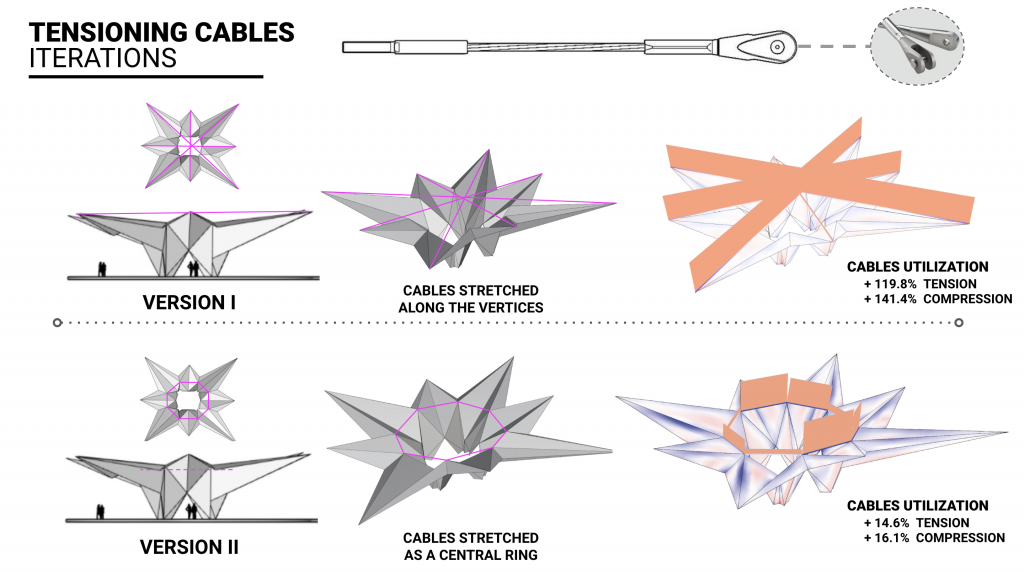
We tested iteration 1, where the cables stretch from the further vertices of the cantilevers all crossing in the center, but also the cables forming an inward circle inside the structure. The latter has shown to be more efficient, so ultimately we added another “ring” of cables to hold the bottom half of the structure as well as the top.
We qu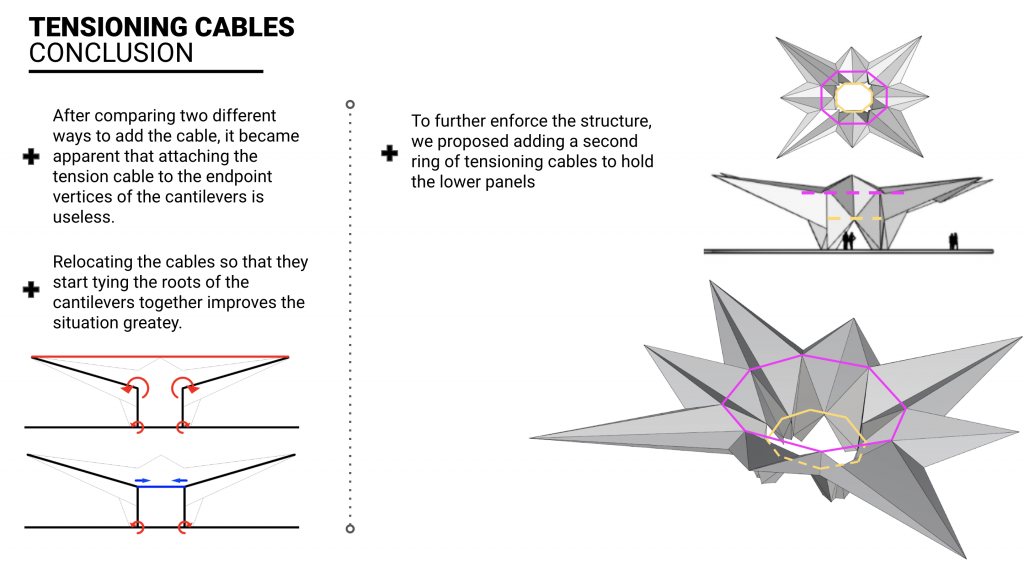
This is a project of IaaC, Institute for Advanced Architecture of Catalonia at MaCad – Master in Advanced computation for Architecture and design in 2020/21 by:
Students: ANDREI OKOLOKOULAK, GERMAN BODENBENDER and SERGEY KRYUCHKOV
Faculty: MANJA VAN DE WORP and HANNA LEPPERØD (Assistant)