The goal of this project was to develop a new way to use recycled tiles from waste’s construction.

References

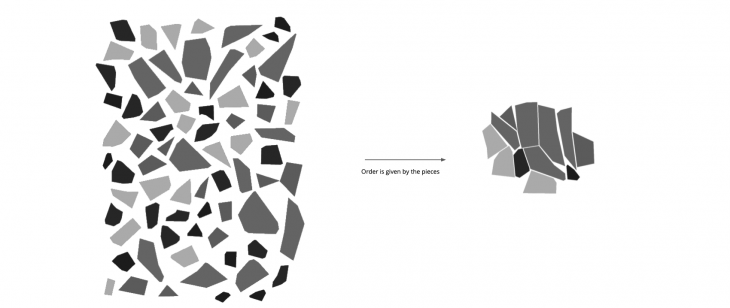
These antic vases gave us an idea to how to organize the mosaics, found the pattern that we wanted to achieve in this workshop.

We understand that exist voids that we have to fill and pieces to join. A trace that organizes something that existed and reconstruct to exist again.

Not always is possible to build the complete figure, but this is an opportunity to learn about the boundaries of the figure. Something that never ends.
The final shape is given by the pieces and how they interact.

Initial Data Set

These are the elements that we have to develop the idea: One tile of 30 by 30, a bunch of pieces and the UR robot.

We decided to choose only one type of mosaic, same color, to be coherent with the idea of reconstruction

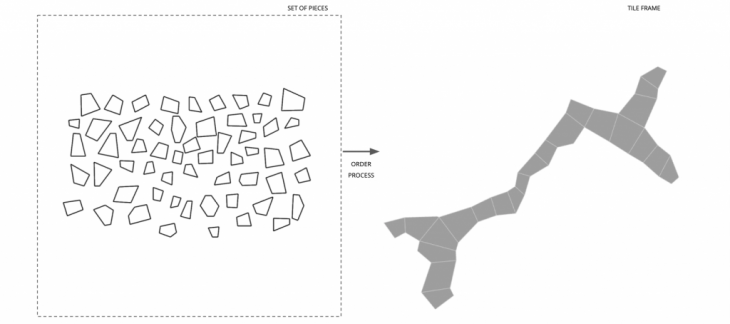
Data Set Process

Then we scan, extract the contours with OpenCV and use this information to develop the final shape with the grasshopper algorithm.

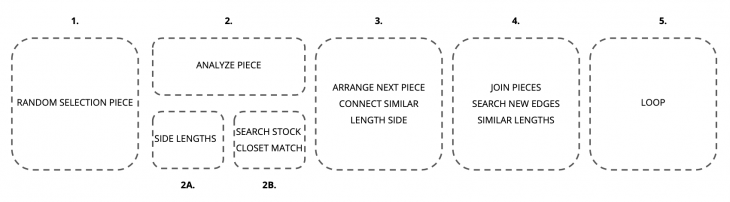
Our first approach was to start analyzing the pieces by quantity of sides, lengths sides and angles. To tried to match the much is possible. We were thinking to start from the center and growing to the tile’s edges.

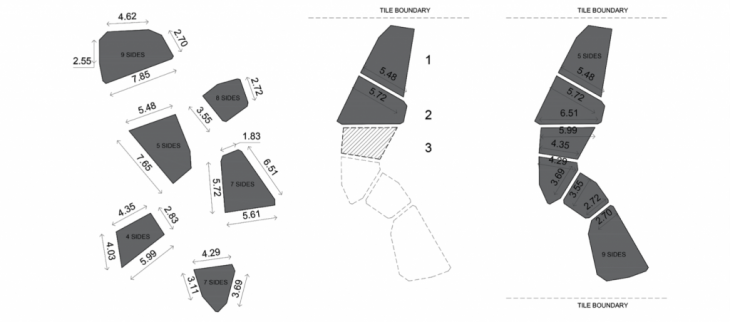
But related to the workshop’s time we decided to start only by the lengths of the piece’s edges. And that was the last criteria to define the design’s pattern.

Manual Exploration

These are examples of manual exploration that help us to understand the rules and logic of the process to then parametrize to digital fabrication.

Diagram Algorithm

Digital Fabrication

Images related to the process and first digital fabrication.

Robotic Mosaic Pattern // Workshop 2.1  is a project of IAAC, Institute for Advanced Architecture of Catalonia developed at the Master in Robotics and Advanced Construction in 2020/2021 by:

Students: Alberto Browne, Michael DiCarlo
Faculty: Angel Muñoz, Alexandre Dubor
Faculty Assistant: Soroush Garivani