Recursive Growth_creepers

Brief:   Recursion in mathematics is stated as a function that is defined by being applied within itself. In other words, the initial conditions are repeated in itself until a satisfactory outcome has been achieved.  The power of recursion evidently lies in the possibility of defining an infinite set of objects by a finite statement. In architecture, the role of recursive has been translated often into a merely aesthetical exploration rather than for solving complex problems with simple rules. This assignment wants to investigate applications and implications of looping and recursive strategies to re frame the generation of architectural spaces.  As a case study students will have to intervene a part of the Mies van der Rohe pavilion and propose an architectural installation applying recursive systems which resembles how would nature proliferate in a contained environment (take over the space).

Concept

To design Structural System above one of the water body of Barcelona pavilion so that on top of which creepers can grow.

Pseudo Code

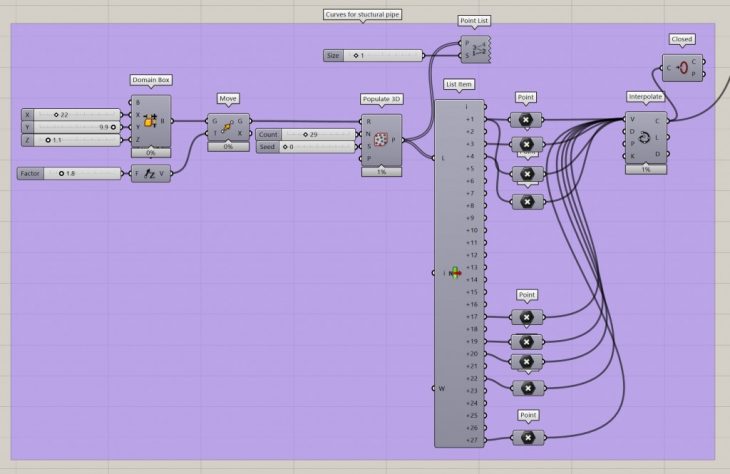
Make closed curve over water body.
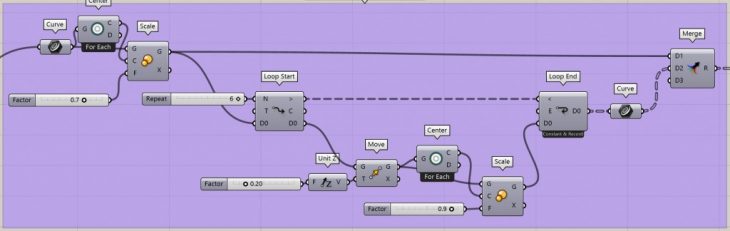
Use Anemon to make more iterations with incremental height from ground and decremented scale.
Give thickness to curve by pipe.
Divide these curves in 6 parts.
Keep parts on which creepers will grow and cull other parts.
Take these parts and further divide them to use points as anchor point for creeper growth.
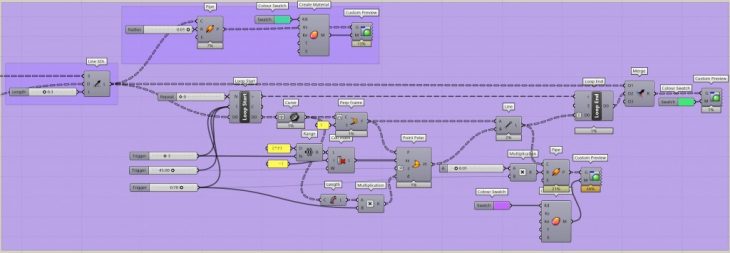
Create lines using SDL starting from those points for branches.
Use end points of previous lines to create more branches.
Use anemone for more iterations.
Give thickness and material where ever it is required.

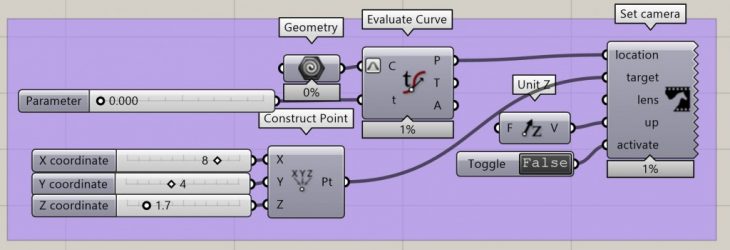
Recursive Growth is a project of IaaC, Institute for Advanced Architecture of Catalonia
developed at Master in Advanced Architecture,
in Year of 2019 by:
Students: Neel Prajapati
Faculty: Rodrigo Aguirre