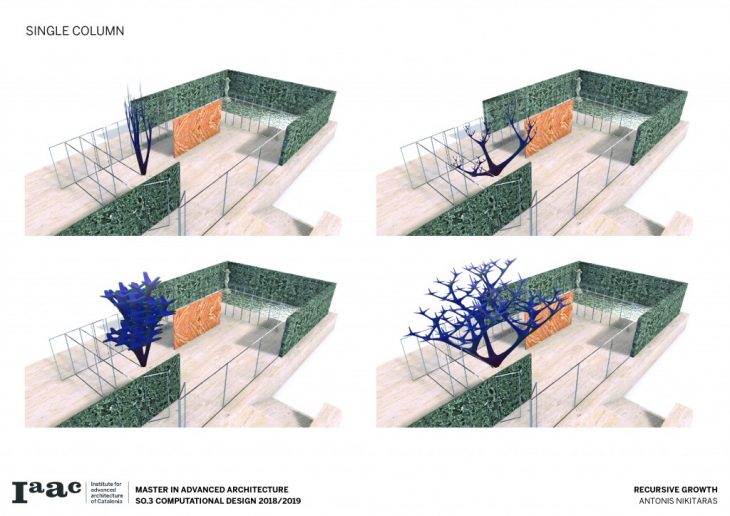
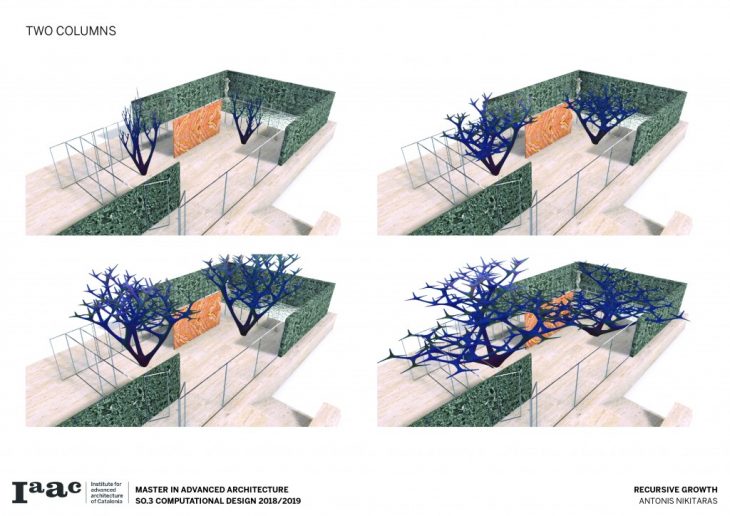
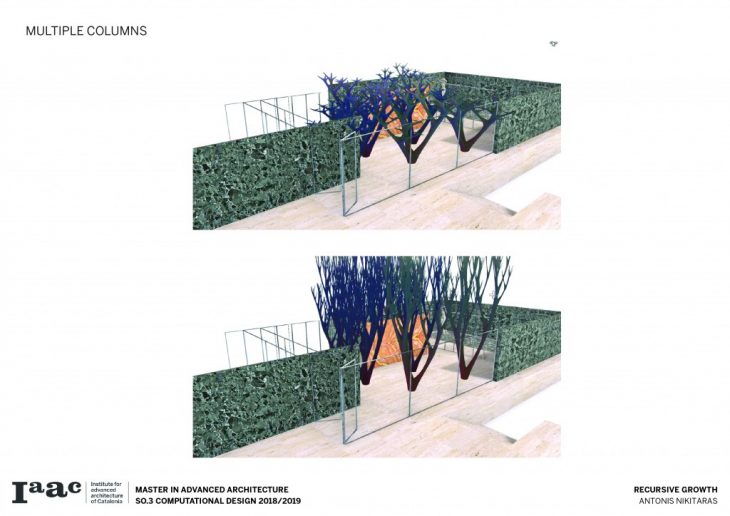
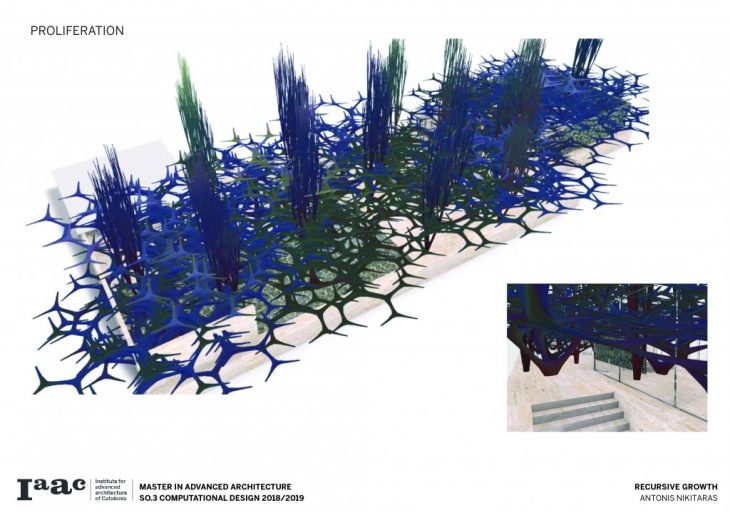
Recursive growth is an attempt to create a column system which has the concept of bifurcation in its basis. Computational techniques aiming towards creating a branching structure are employed, looking at two different scopes. On the one hand a large scale architectural application is explored, looking at how this bifurcated system can be applied to a structure of large volume. Inspired by the work of Antoni Gaudi and the famous columns of the Sagrada Familia in Barcelona, the columns are articulated by the use of certain profiles and branch out to cover large spans. On the other hand, recursive growth is being looked at a smaller scale, situated in the Mies van der Rohe pavilion, also in Barcelona, in an approach of growth going out of control and proliferating, taking over the pavilion.

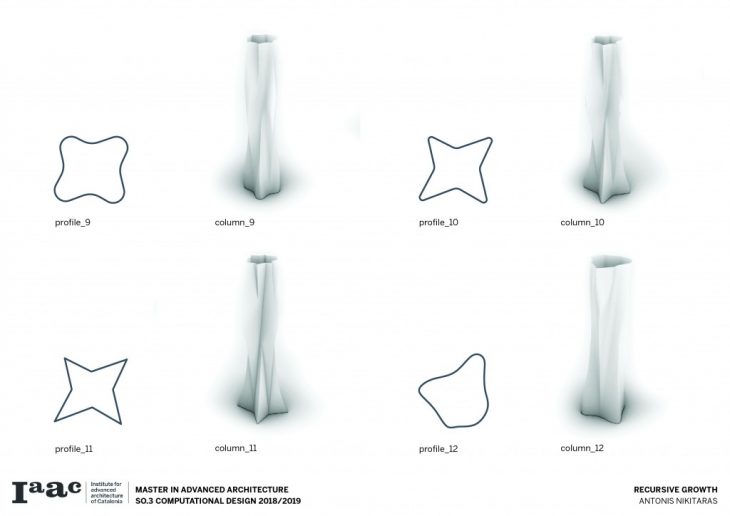
The first step of the project involves articulating the surface of the column by using a set of profiles which rotate as they move along the length of the column, carving out material and resulting in these expressive surfaces.

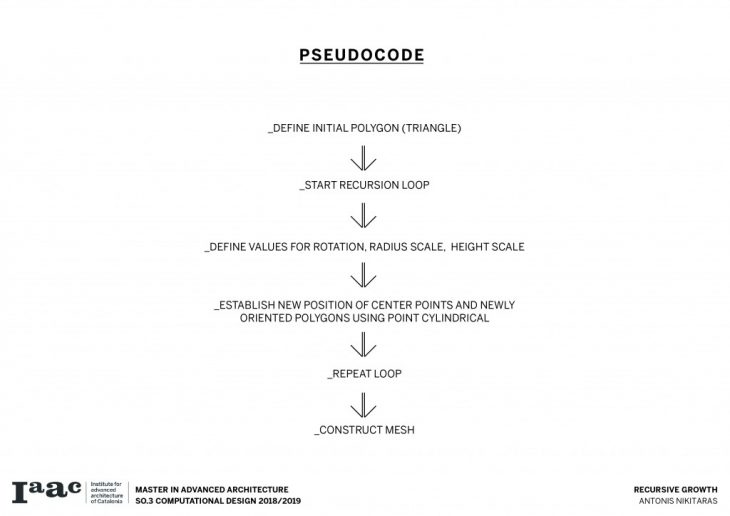
The branching of the columns is achieved through a computational technique recreating the idea of the L-systems. L-systems are essentially a mathematical process to achieve recursion, often used to recreate branching phenomena in nature.

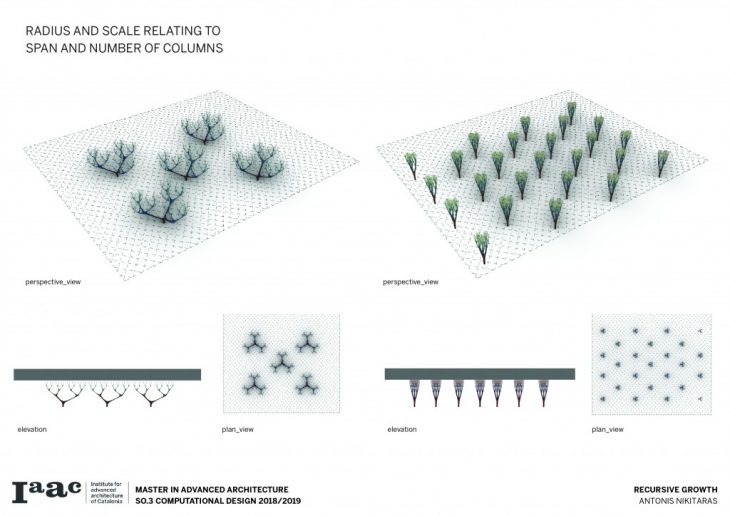
Consequently a catalogue is created with variable scale, radius and height, in order to understand and visualise the possibilities of this techniques and all the different variations which can be parametrically achieved by changing a certain set of parameters.

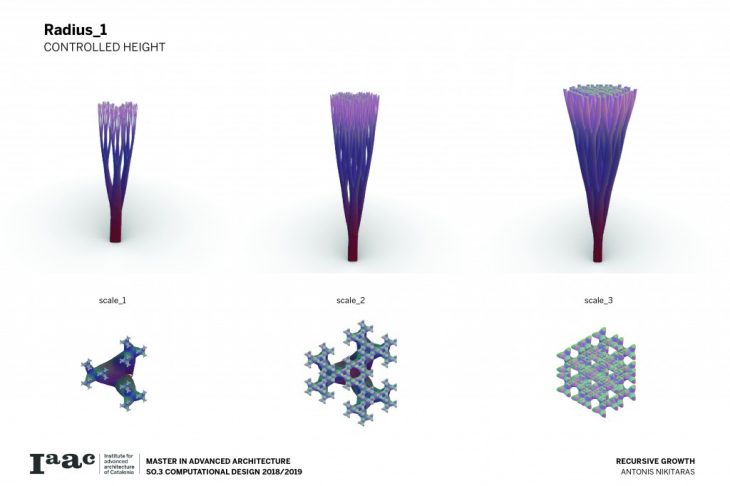
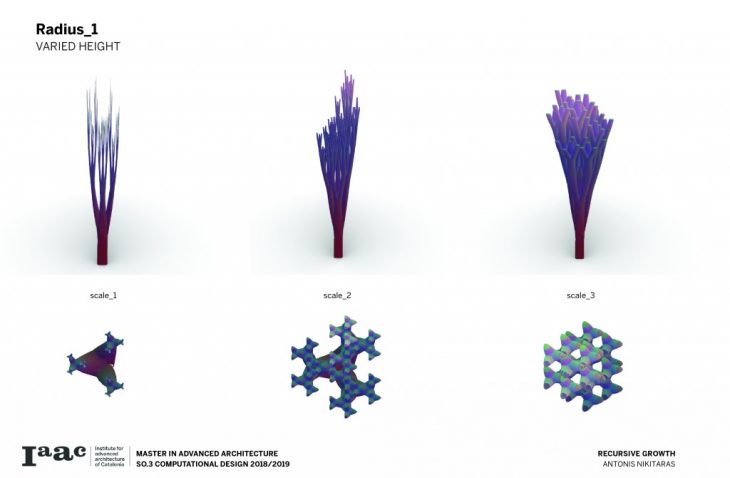
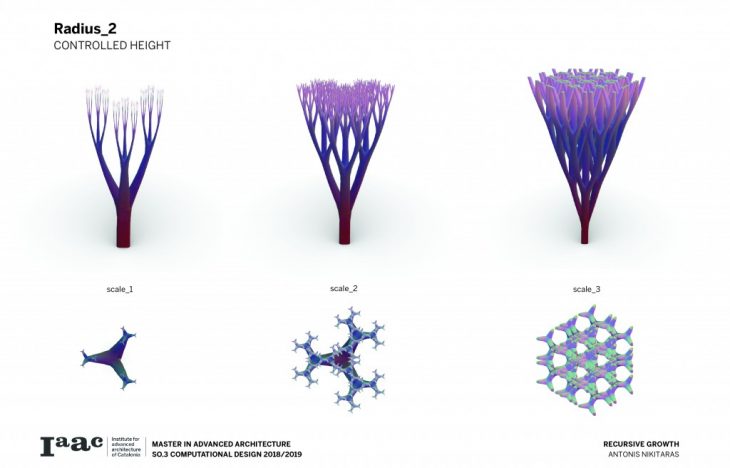
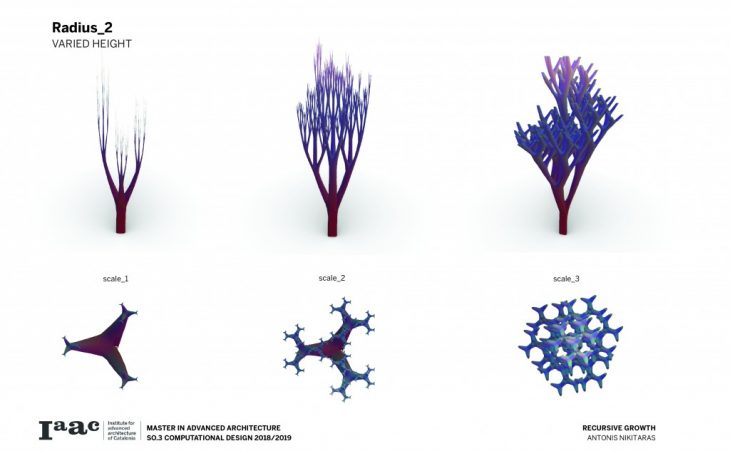
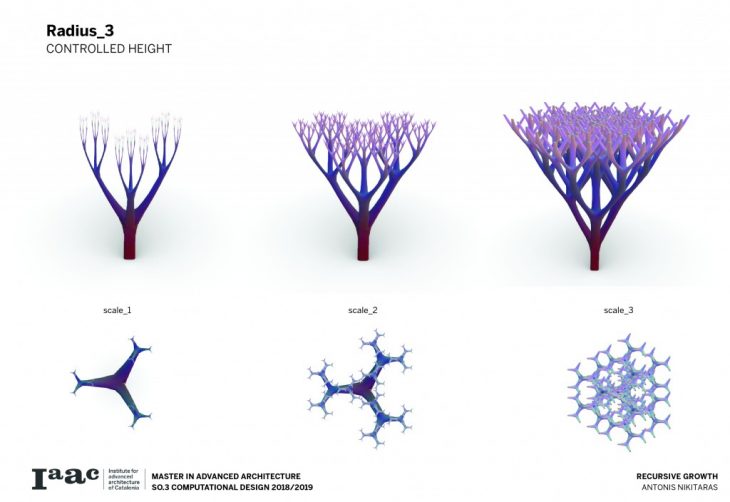
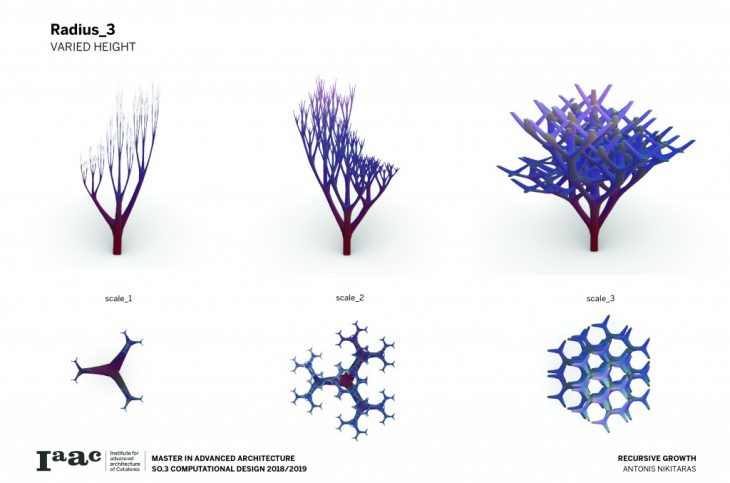
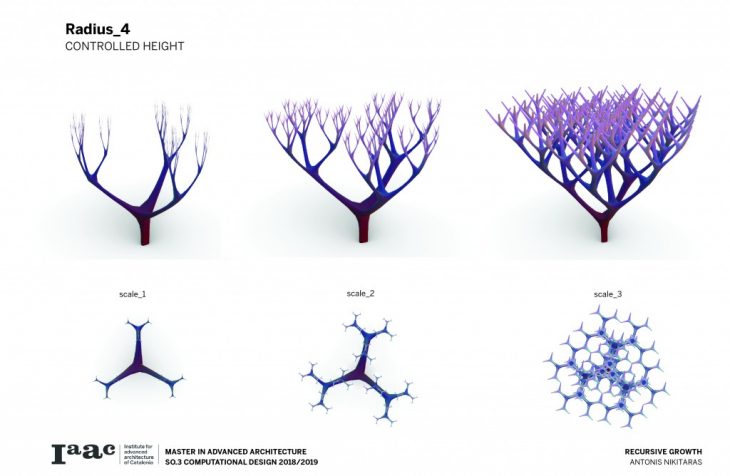
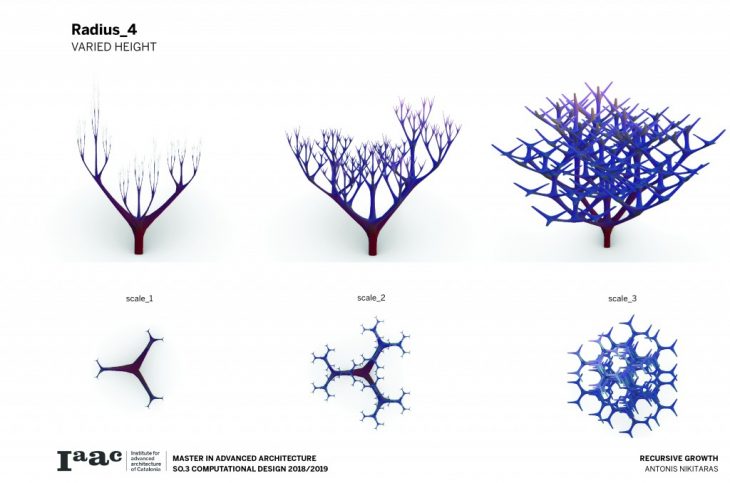
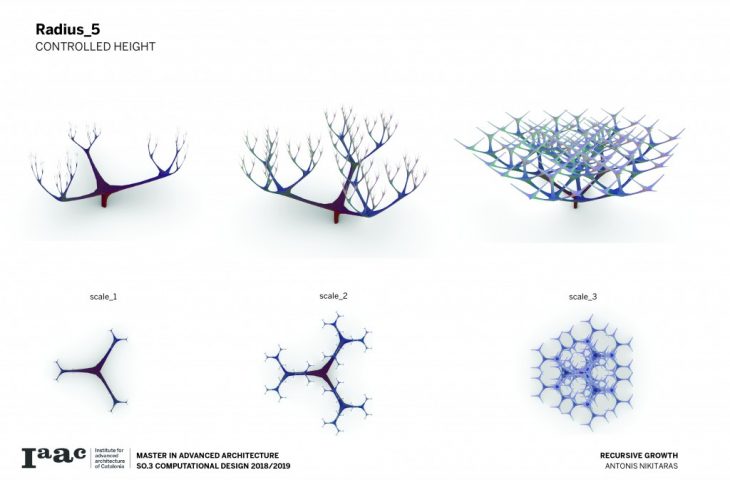
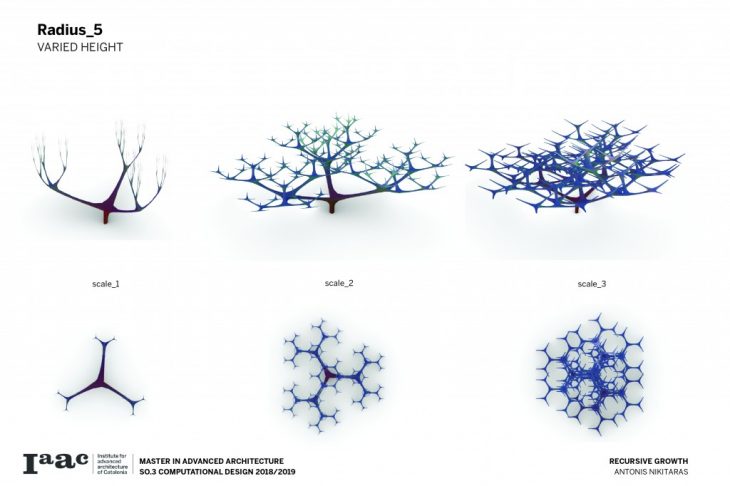
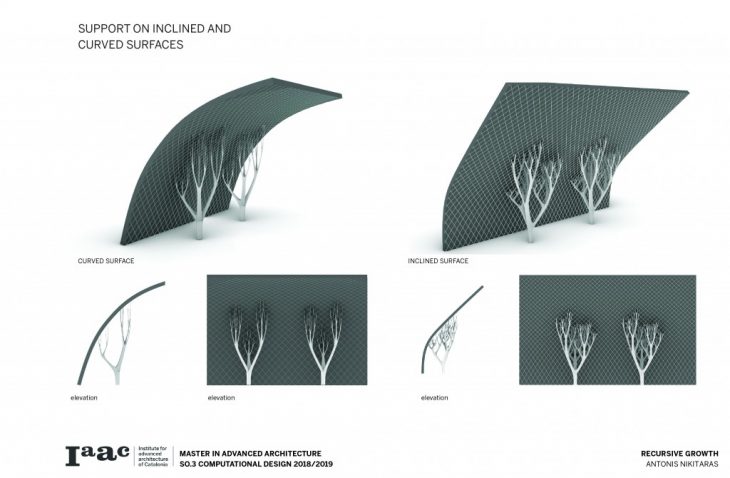
The architectural application involves the use of the columns to support large spans and complex forms.

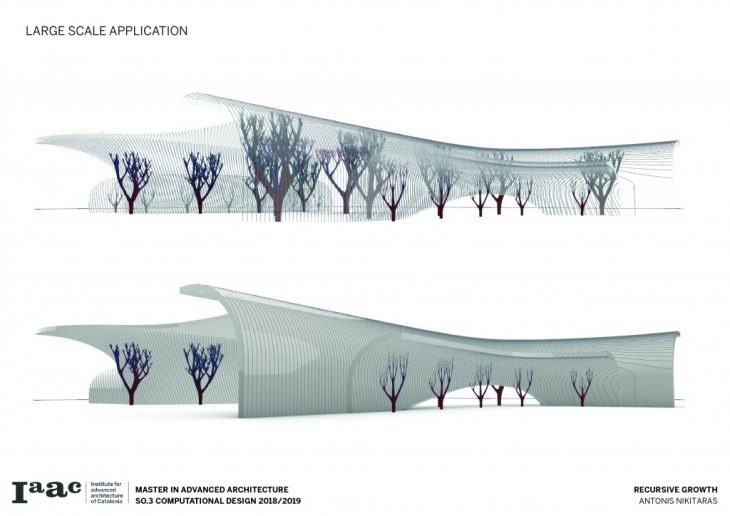
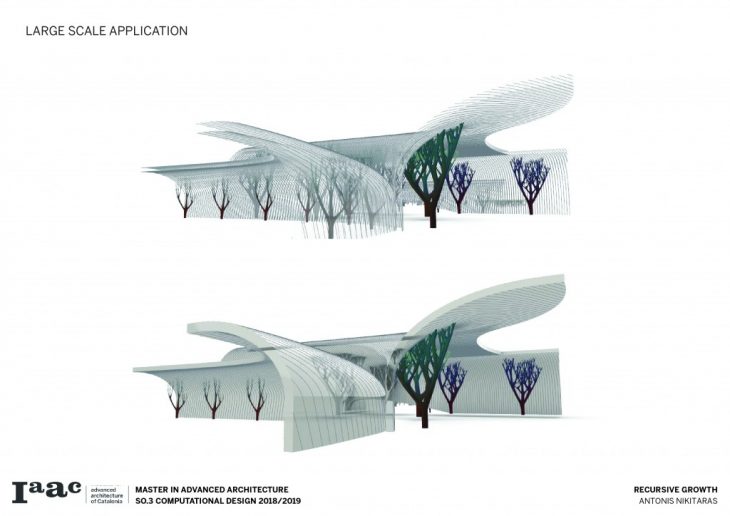
Finally recursive growth is applied in the Mies van der Rohe pavilion starting from a single column and gradually adding more, until the system proliferates and completely takes over the pavilion.