RANDOM [WALKER]
The term random walk was first introduced by Karl Pearson in 1905. A random walk is a
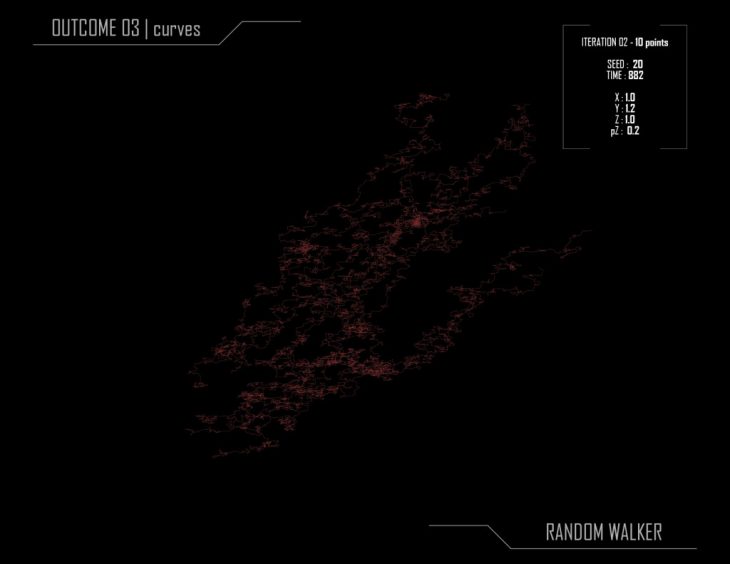
mathematical object, known as a stochastic or random process, that describes a path that consists of a succession of random steps on some mathematical space such as the integers. An elementary example of a random walk is the random walk on the integer number line Z which starts at 0 and at each step moves +1 or ?1 with equal probability.

Random walks have applications to engineering and many scientific fields including ecology, psychology, computer science, physics, chemistry, biology as well as economics. Random walks explain the observed behaviors of many processes in these fields, and thus serve as a fundamental model for the recorded stochastic activity. As a more mathematical application, the value of ? can be approximated by the use of random walk in an agent-based modeling environment.

The code development is based on the following methodology: 1.Generate a start point / 2.Create a random number between -1 and 1 / 3.Assign each the x,y, and z axis one of random numbers / 4.Assign each the x,y, and z axis one of random numbers / 5.Take a step in that direction.
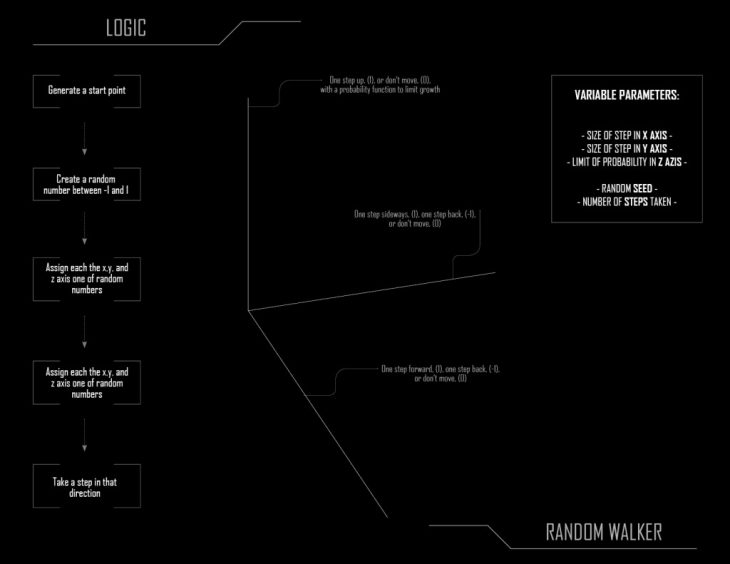
VARIABLE PARAMETERS:
– SIZE OF STEP IN X AXIS –
– SIZE OF STEP IN Y AXIS –
– LIMIT OF PROBABILITY IN Z AXIS –
– RANDOM SEED –
– NUMBER OF STEPS TAKEN –


The random walker algorithm is an algorithm for image segmentation. In the first description of the algorithm, a user interactively labels a small number of pixels with known labels (called seeds), e.g., “object” and “background”. The unlabeled pixels are each imagined to release a random walker, and the probability is computed that each pixel’s random walker first arrives at a seed bearing each label, i.e., if a user places K seeds, each with a different label, then it is necessary to compute, for each pixel, the probability that a random walker leaving the pixel will first arrive at each seed. These probabilities may be determined analytically by solving a system of linear equations. After computing these probabilities for each pixel, the pixel is assigned to the label for which it is most likely to send a random walker. The image is modeled as a graph, in which each pixel corresponds to a node which is connected to neighboring pixels by edges, and the edges are weighted to reflect the similarity between the pixels.



RANDOM [WALKER] is a project developed at IaaC, Institute for Advanced Architecture of Catalonia, developed at Master in Advanced Architecture 2019/20 by:
Students: Holly Carton, Daria Ciobanu-Enescu, Eszter Olah, Oana Taut
Faculty: Angel Munoz