Introduction
Mechanical metamaterials are artificial structures with mechanical properties defined by their structure and material, rather than their composition. They exhibit properties not found in natural materials, such as a negative Poisson’s ratio.
Origami Metamaterials combine the japanese art of paper folding to create metamaterials that have properties derived from both the properties of the sheet material and geometric arrangement of the folding. The physical properties of origami metamaterials, in particular the Miura-Ori fold, have been recently researched. These metamaterials can be used for a variety of applications in the realm of product design including soft robotics, aerospace, civil engineering structures, and safety equipment.
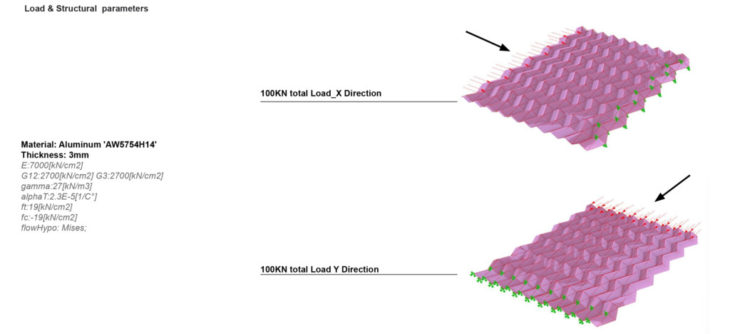
Origami has been employed in the creation of deployable metamaterials that fold and unfold along the crease lines. The desired deployability and collapsibility of these metamaterials are often controlled through a tunable stiffness parameter. The stiffness, k of a body is a measure of the resistance offered by an elastic body to deformation and for origami metamaterials, it is determined by the displacement and degree of freedom of its vertices, and applied load.
In this project we will try to predict the displacement of Miura-Ori based origami metamaterials.
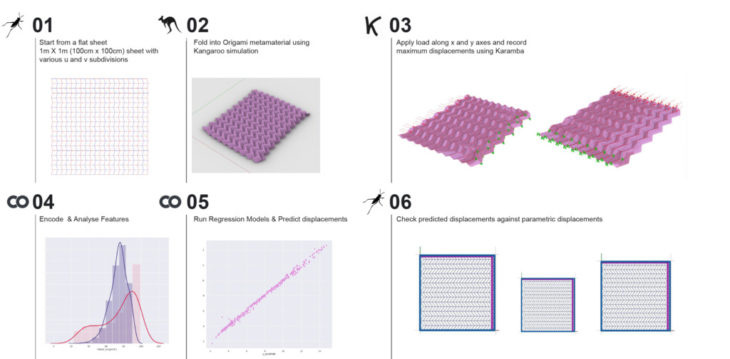
Process
Parameterizing Origami
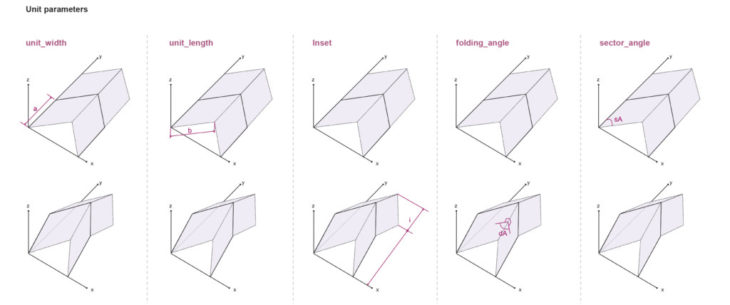
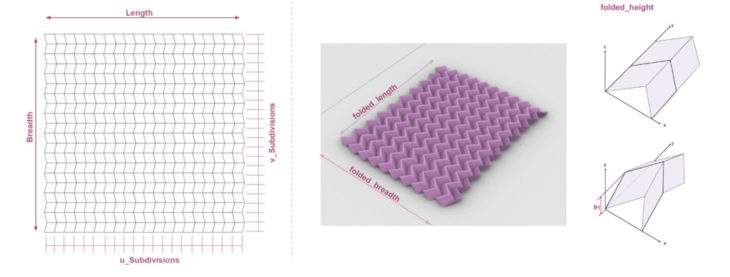
Parameters of Miura-Ori tessellation
Datasets analysis & feature extraction
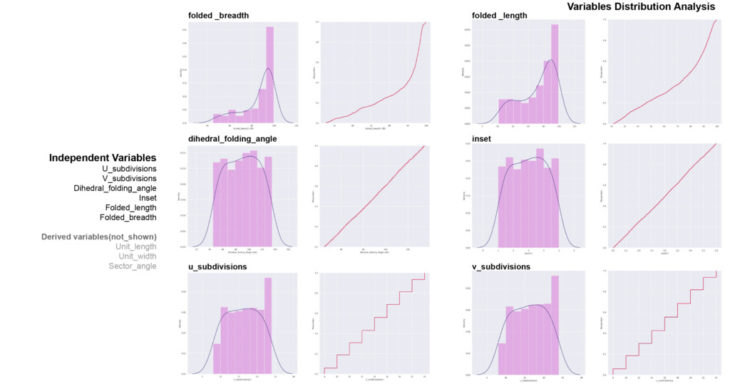
Independent variables
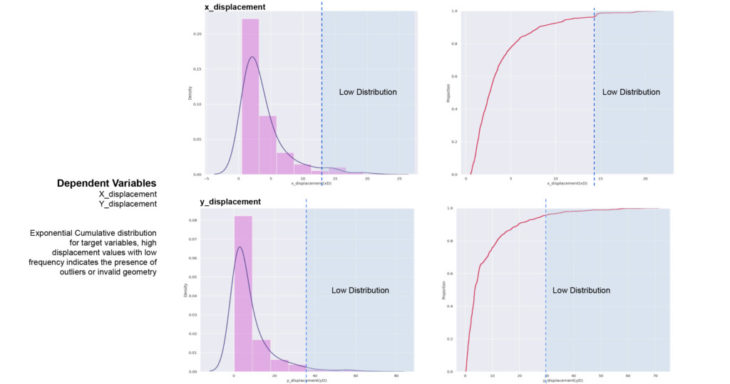
Dependant variables
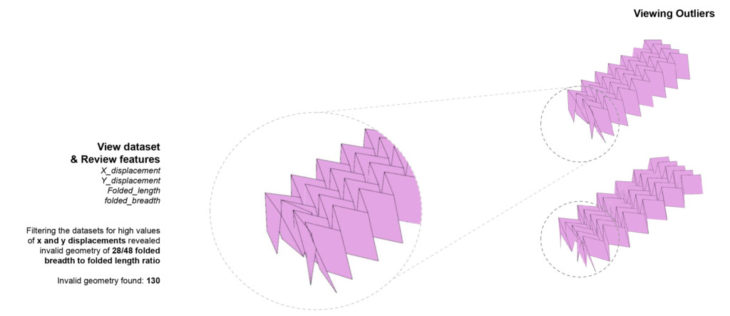
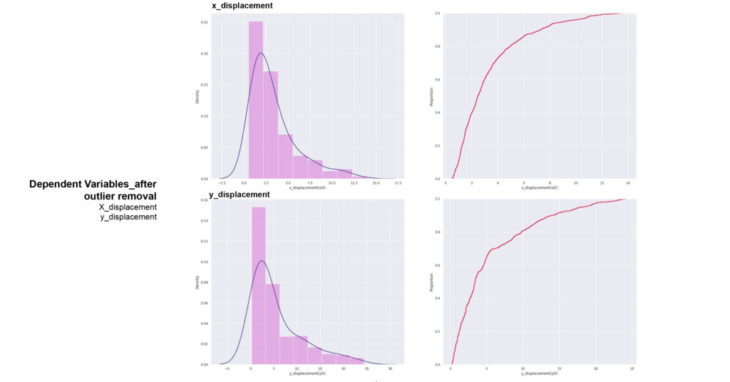
Observing that the predicted values are still not equally distributed even after the removal of outliers, we decide to augment the dataset through Kohonen maps, and see whether it influences the accuracy of the models.
Training

Used machine learning models
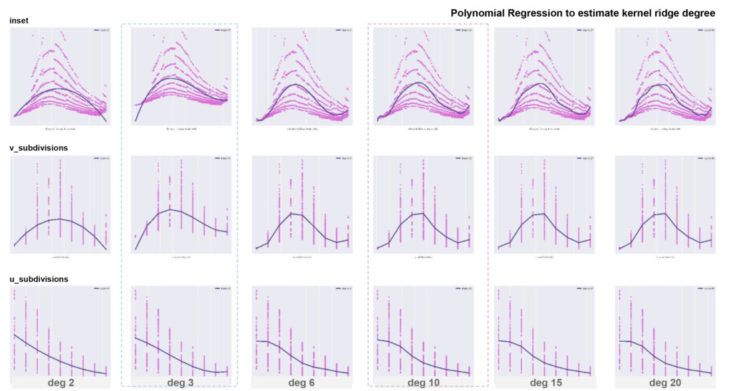
Observing the pairplots of the variables and the predicted values, we understand that the relationship is polynomial. We conclude that right kernel degree is 6, kernel ridge degree 3 might underfit while degree 10 overfits.
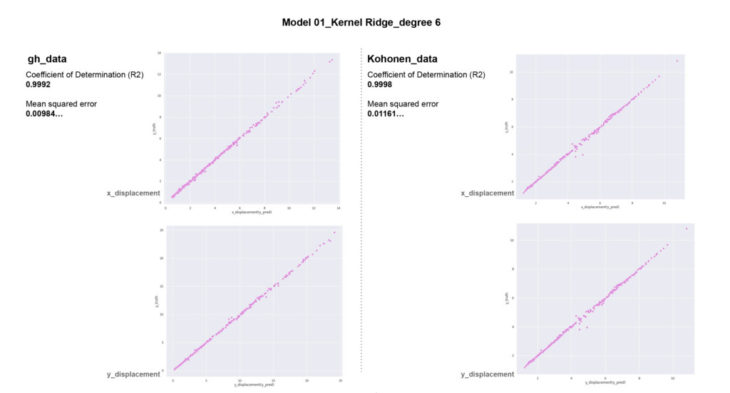
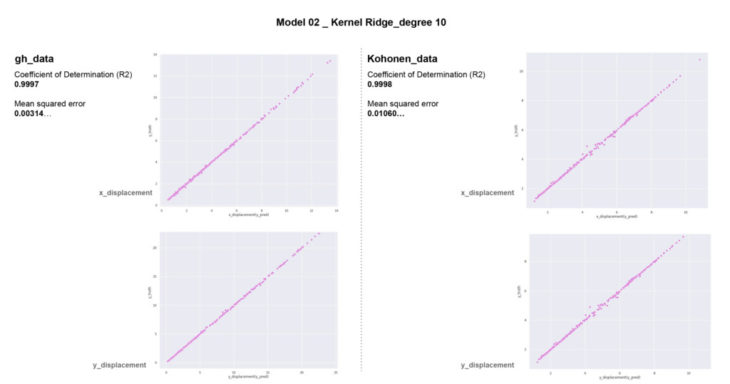
Kernel Ridge model
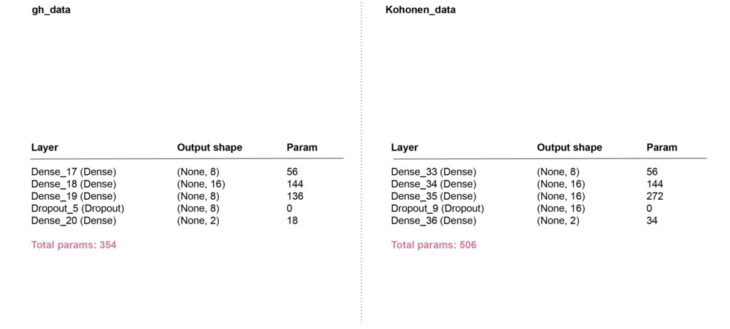
Neural Network
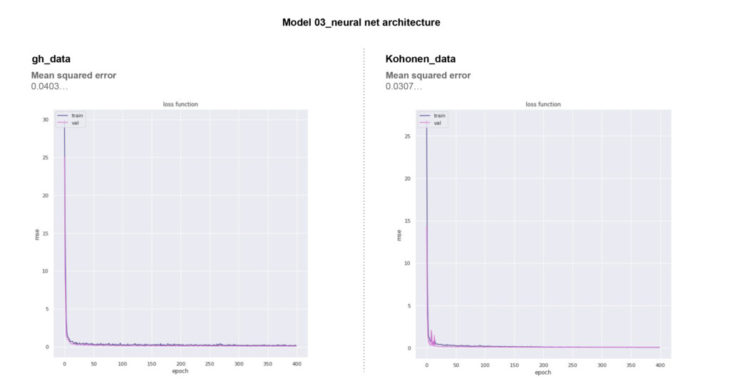
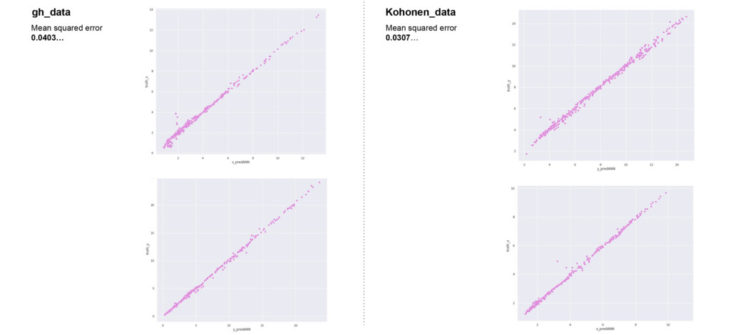
The kernel ridge model performs best.
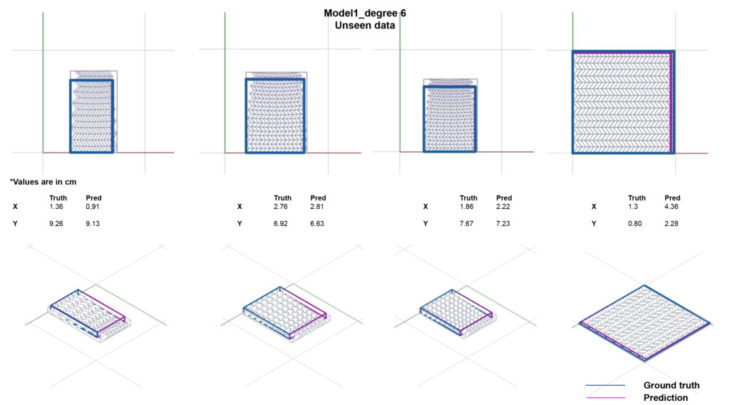
Grasshopper comparison
Testing the models in grasshopper we can conclude:
In the range the model has been trained on:
Differences of displacements are in the range of 5 mm, within tolerances of the thickness of material.
In other ranges :
Predicted displacements are not reliable, especially in cases of big values of subdivisions and plane dimensions.
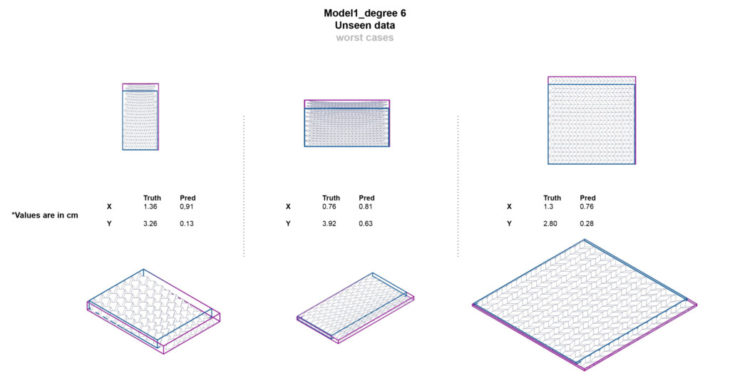
Next steps would include expanding the ranges of values in the dataset and introducing different materials and sheet dimensions.
Predicting displacement of Origami Metamaterials is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Master in Advanced Computation for Architecture & Design 2021/22 by students: Oluwadamilola Akinniyi, Erida Bendo and faculty: Gabriella Rossi and Hesham Shawqy.
