Objective
In Geometry Optimization seminar, part of the third module of IAAC’s MaCAD, we were exploring various strategies of surface rationalization and how to optimize for digital fabrication. We were learning tools like GH Python and Hops to assist with bringing Python libraries like NetworkX and Flask scripting into Grasshopper 3D environment As a group, we were interested in ways to encode data into the fabrication and rationalization processes.
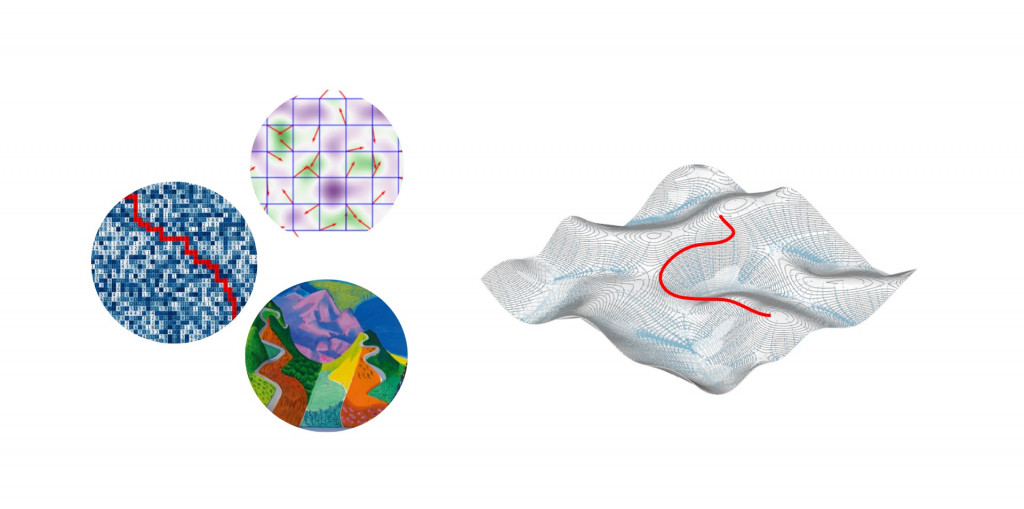
As we are both passionate about music, we wanted to encode music as a pattern for fabrication. We were inspired by a musicbox that reads an encoded patter of holes or dots that represent musical notes on a strip of paper.

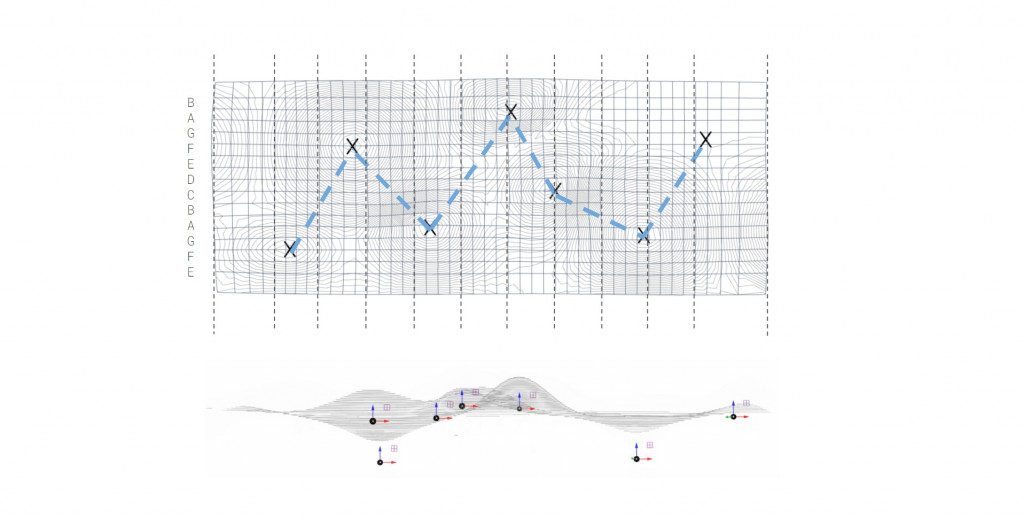
We decided to adopt that approach and translate Bethoven’s Fur Elise into a 3D terrain. X axis represents time, Y – pitch and Z velocity. We then fine-tuned the z axis to get a landscape we enjoy to essentially make a walk between the music notes.
Rationalization
The music walk essentially becomes a sequence of shortest paths between the points. Once we have defined the path we removed it from the mesh to preserve its shape.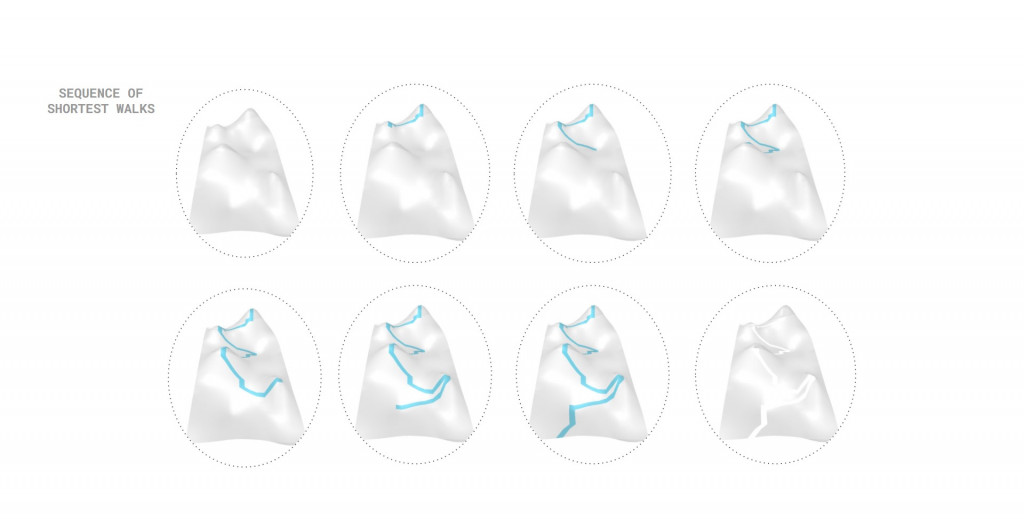
We then had to figure out a way to generate strips that make up the remaining geometry. We initially looked at “minimum spanning trees” as it seemed like an appropriate way to encode information while rationalizing the geometry. In the image below you can see red and yellow dots that represent the beginning and the end of the tree. By connecting the dots we could generate stripes that preserved the flow of the spanning tree.
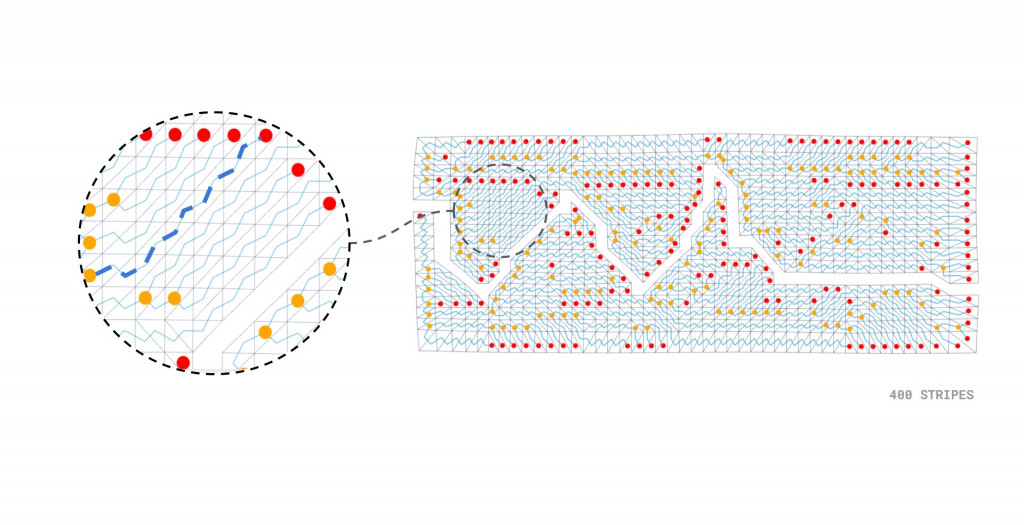
The initial approach resulted in a messy set of many stripes that looked random and included singular triangles.

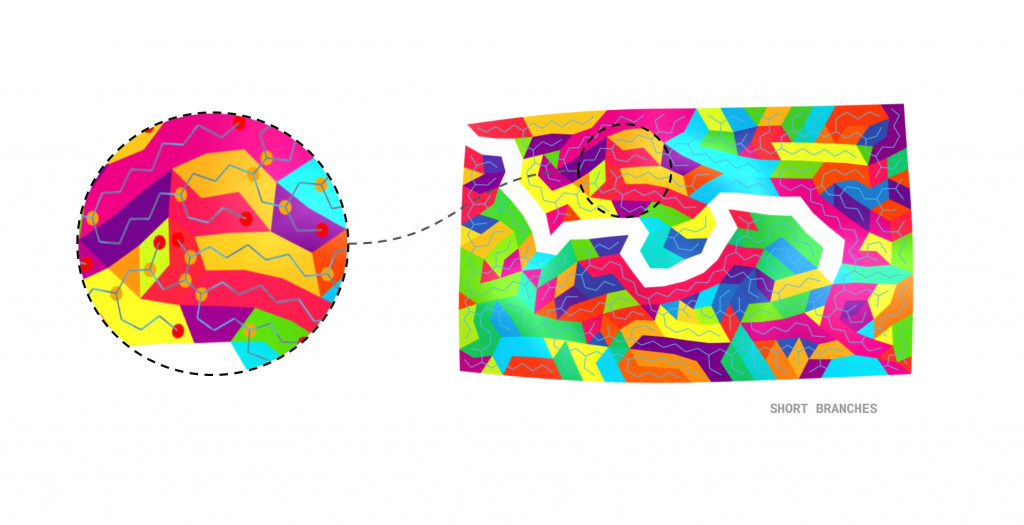
We decided to reduce the size of the landscape and noticed the minimum spanning trees pattern becomes quite erratic with shorter branches that constantly changed direction. The result still generated a lot of stripes and singular pieces.
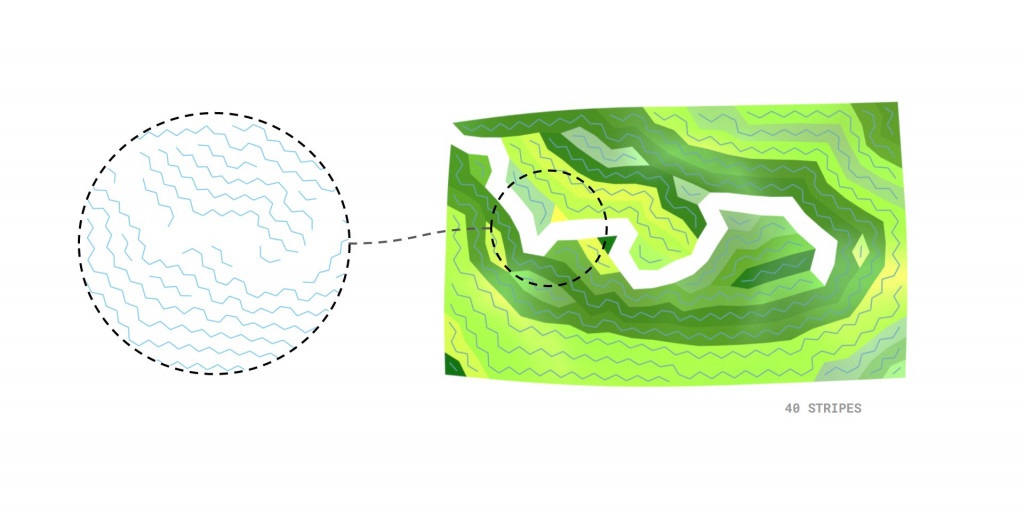
We tried another approach where the landscape is divided into strips of longest walks, which drastically reduced the amount of used strips.
Fabrication
Below is the final geometry that represents our musical landscape with the white stripe that encodes notes of Bethoven’s Fur Elise connected by shortest paths.

As the last digital step before fabrication, we unrolled the geometry into strips using OpenNest plugin. We labeled start and end of the strip and offsetted the edges.
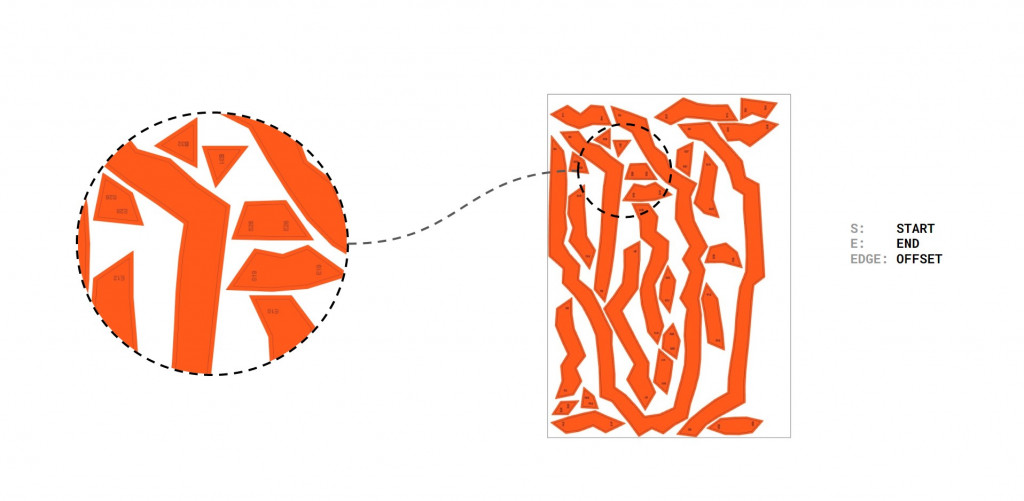
Then the challenge of fabrication began. Being restricted to home materials and A4 printer, we faced various challenges of achieving a free standing shape.

Credits:
Students:
Andrei Okolokoulak, Joao Silva
Faculty:
David Andres Leon, Dai Kandil