TIMBER IN TENSION
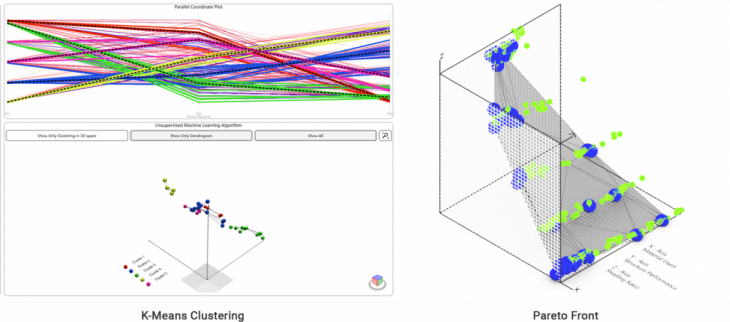
GENETIC OPTIMIZATION – Theory of Natural Evolution.
The project aim is generate a the most optimal solution in the architectural element or environment. Here, algorithms reflects the process of natural selection where each individuals are selected for the reproduction in order to produce descendant of the next generation.
Project Concept
Multi Objectives Optimisation & Ruled Surfaces
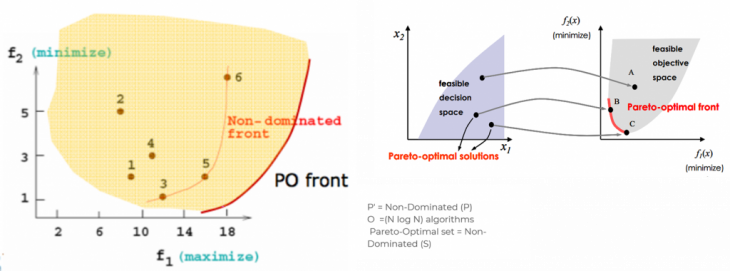
- – Involve more than one objectives function that are to be minimized or maximized.
- – In multi-objective optimization problem, the solution is determined by the dominance.
- – So instead of dominance solution we can use the non-dominated set of solutions for the entire feasible space is called the Pareto-optimal set.
- – Pareto Optimal is to find possible set of solution in diverse parameters.
- An exploration into genetic optimization with the concept of Hyperbolic paraboloid surfaces.
- Structure benefits because of the Gauss curvature of such surfaces is not zero.
- Bending the shape strengthen the structure.
Pseudo code
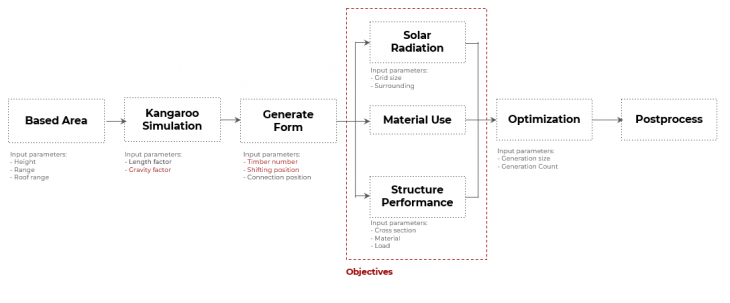
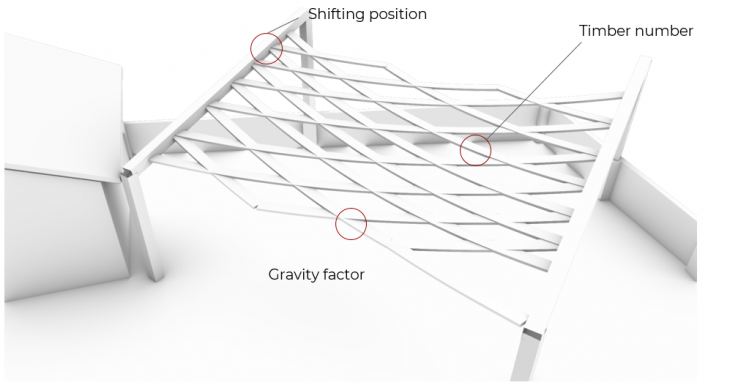
Input Parameters
Script
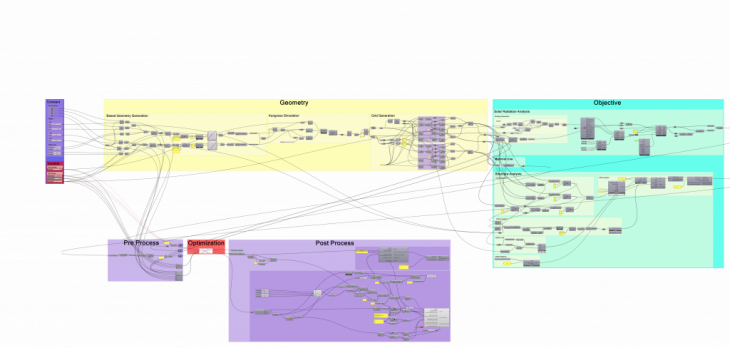
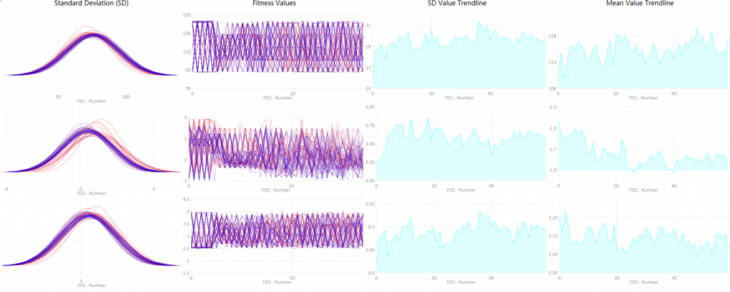
Optimisation Results
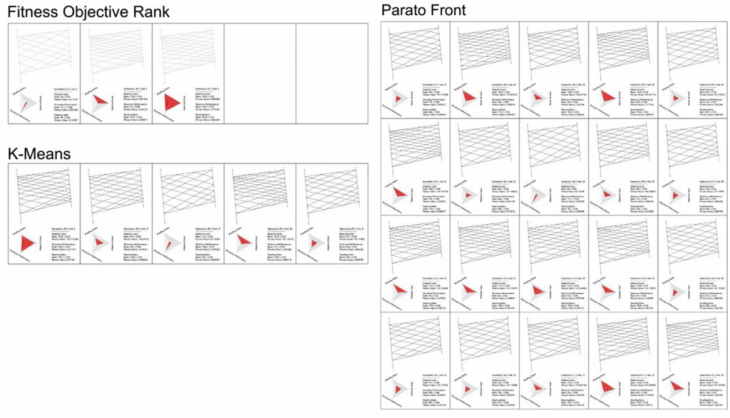
Catalog
RENDER

CREDITS
GENETIC OPTIMIZATION is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Master in Advanced Architecture 2020/21 by Students: Elizaveta Veretilnaya, Liang Mayuqi, Stefanie Eleonore Thaller, Lekha Gajbhiye, Tullio Polisi
Faculty – Rodrigo Aguirre, Assistant – Ashkan Foroughi