ABSTRACT

In the age of artificial intelligence (AI) and machine learning (ML), architects always look for digital aids, that helps them identify building performance and characteristics at an early design stage but going through every design iteration and performing same repetitive task can be counter-productive. This research thesis explores a conceptual workflow to classify 3D prototypes of building forms based on their topological relationships. The thesis focuses on developing graph machine learning (GML) system that learns from its architectural precedents based on its topological graphs. This conceptual workflow consist of three primary steps. First one is to construct synthetic dataset based on the architectural precedents. The building dataset are generated using parametric modelling. Second step, is to encode graphs in the building dataset. And the final step is to use the supervised graph machine learning model using Graph Convolution Networks (GCN). This thesis demonstrates the potential of a machine learning based recommendation system that will allow designers to classify the topology of their architectural solution.

CONTEXT

Existing building forms around the world

There were plenty of building forms seen around the world, some of them that identified here were townhouses, row houses, courtyard houses, shophouses, residential apartments (Narkomfin Building, Russia) and high-rise towers.

TYPOLOGY-1 (Slab Building)

Typology-1

Slab building is the typology which has a corridor in the center flanked by units/flats/rooms on both the sides.

TYPOLOGY-2 (High-Rise Building)

Typology-2

High-rise building is the typology which has core in the center surrounded by 4 units/flats on all the four sides.

Typology-3 (Perimeter Block)

Typology-3

Perimeter block is the typology that has courtyard in the center surrounded by the units/flats and corridor around it.

How can building spaces be abstracted and represented?

BUILDINGS AS TOPOLOGICAL GRAPHS

Seven bridges of Konigsberg

The first theory on abstraction of physical space was set by Leonard Euler in 1763 who used topolocal graphs to arrive to his negative solution of the Seven Bridges of Konigsberg problem. These qualities make topology an efficient mechanism for systematically abstracting space and form into topological graphs.

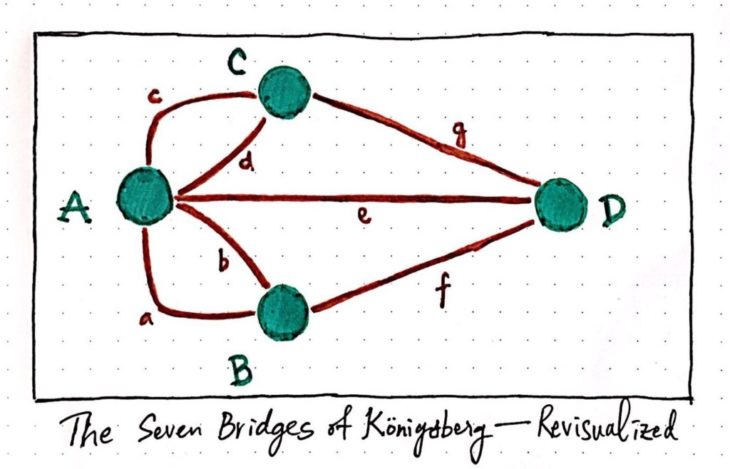
Topology is a mathematical field concerned with the properties of a geometric object that are preserved through continuous deformations such as stretching and twisting.

SPACE SYNTAX: Bill Hillier’s theory of Configuration

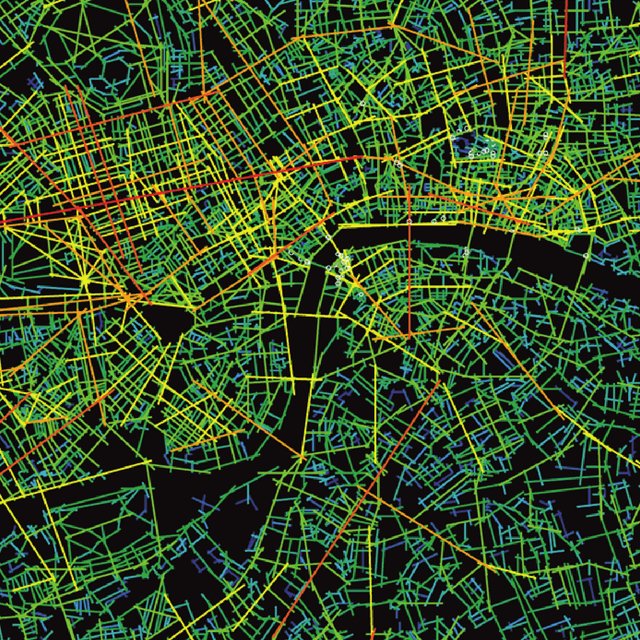
Space syntax street centrality analysis of central London

TOPOLOGICAL GRAPHS

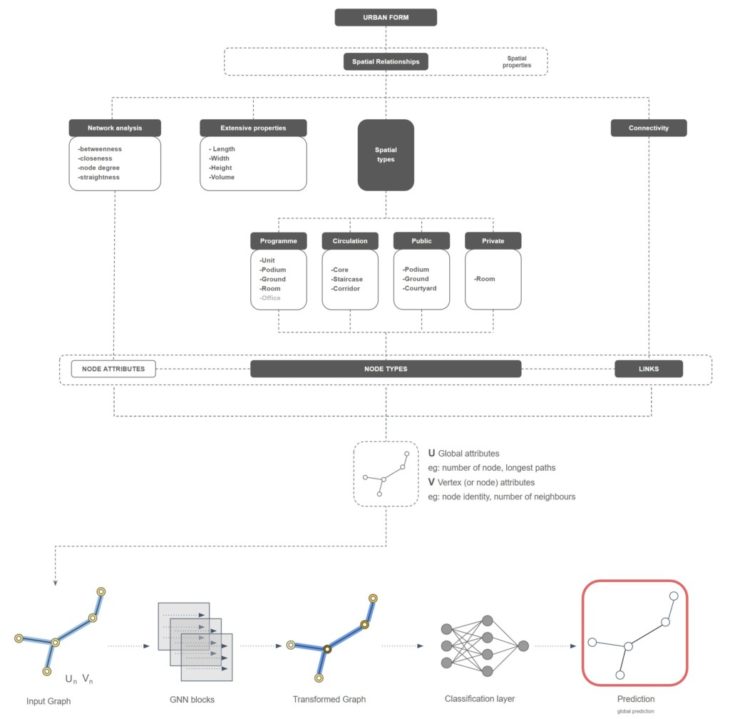
To start building topological graphs the building spatial information extracted and transformed into spatial networks using topological adjacency graph. A graph in which the vertices and edges are the spatial elements associated with geometric objects. To construct the spatial network the space must be deconstructed into its relevant properties. The spaces defined in the previous datasets like courtyards, units/rooms/flats, corridors, building core, podium and ground become the different node types classified under circulation, private, public and external circulation space. The links between these are also classified as walkable, floor and wall based on the two nodes they are connecting. Eventually the link classification is not used in the machine learning process and only the task of graph classification is used in this thesis.

Below are the example of topological graphs for the three typologies setup earlier.

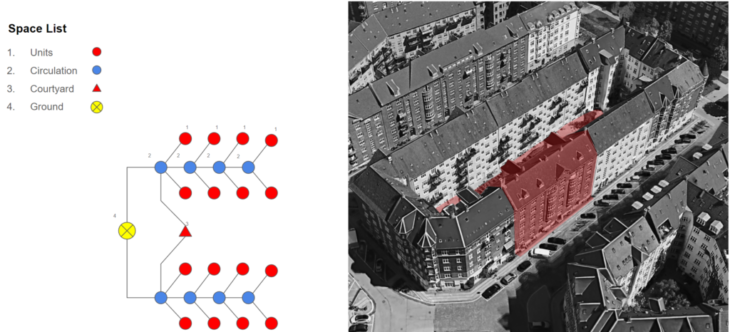
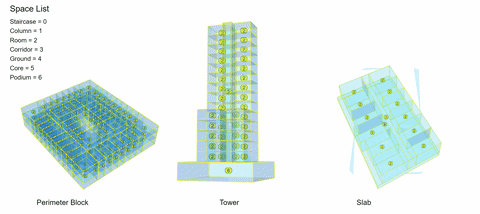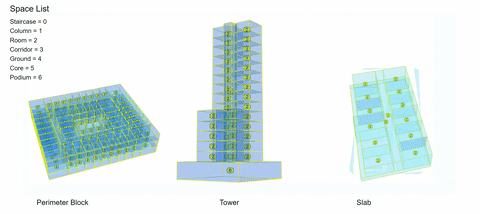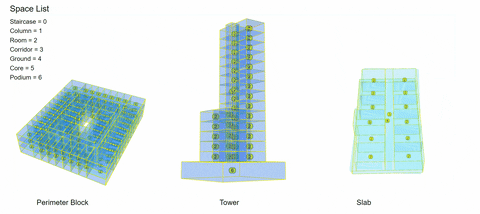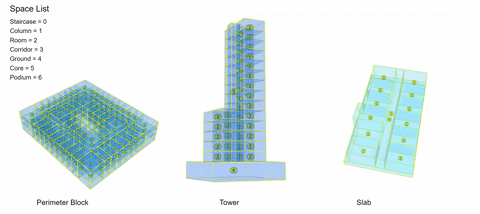
Perimeter Block

The perimeter block shows the connection of courtyard with the ground; ground connected to circulation corridor; and corridor flanked by two flats on both the sides.

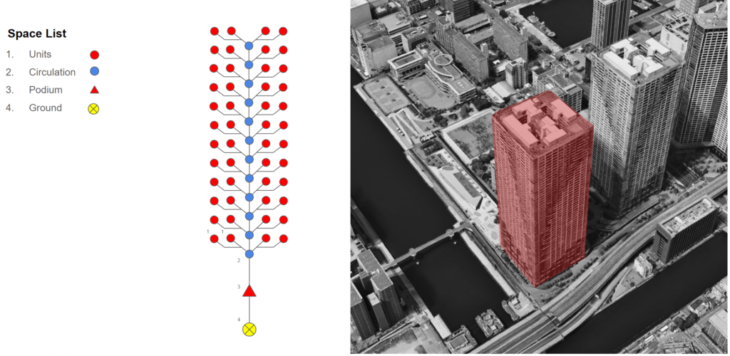
High-Rise Tower

High-rise tower shows the building central core connected to the podium; podium connected to the ground and all the flats connected to the central core.

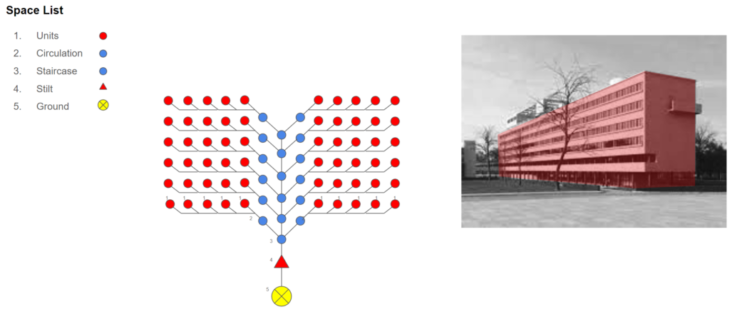
Slab Block

Slab block shows a stilt floor connected to the ground; stilt floor connected to the staircase (vertical circulation); staircase connected to circulation corridor on every floor; corridor connected to ‘n’ number of flats on both the sides.

TECHNOLOGY

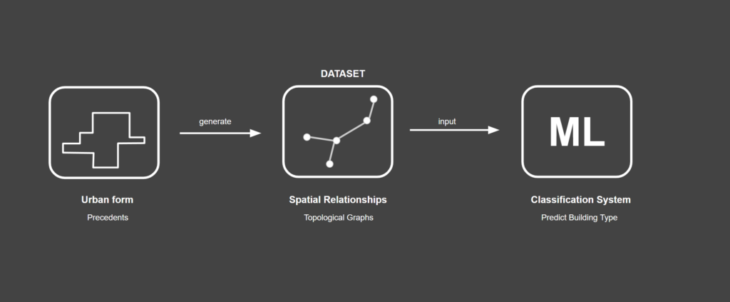
The technology that is used for realising this conceptual workflow is based on three key steps. First is the creation of different urban forms i.e. the different typologies. This part involves creation of dataset; multiple buildings depicting similar topological connections are created for different topologies. Next part is encoding the graphs that show the spatial relationship (Topological Graphs) are generated (from the previously created building dataset). The final part involves inputting these graphs into the machine learning system (Classification system). That will eventually predict the building type.

Urban Form

VARIABLE PARAMETERS IN GRASSHOPPER WORKFLOW

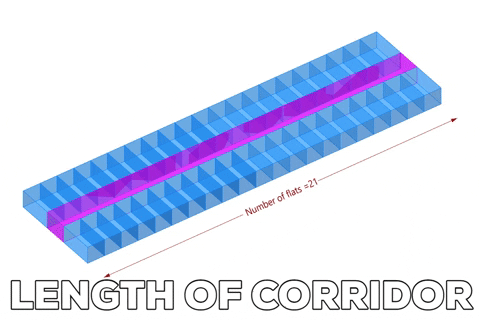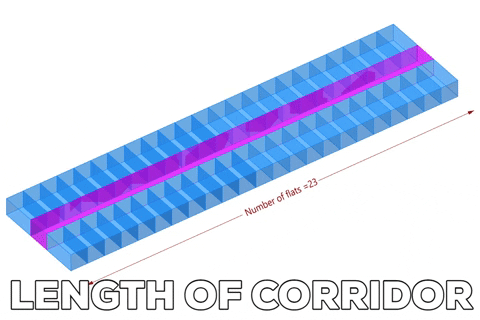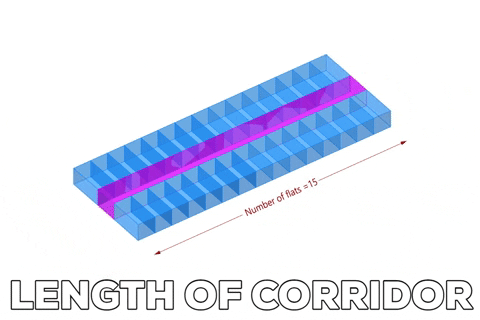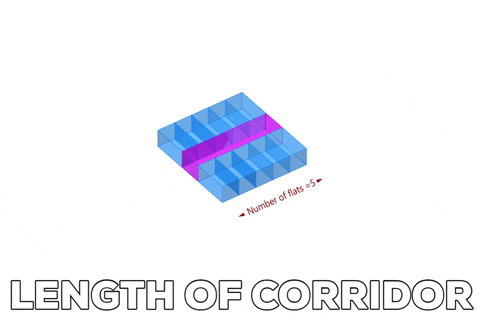Variable length of corridor depends on the number of flats in x-direction.

Building core height varies according to the number of floors in the tower building.

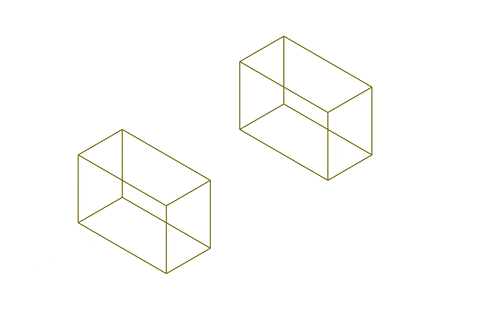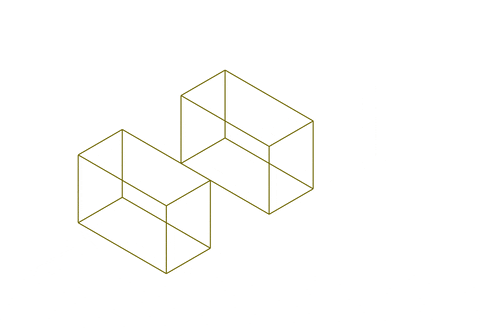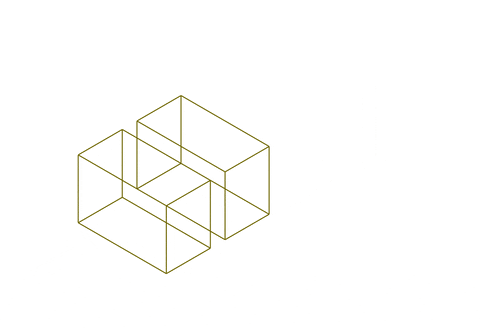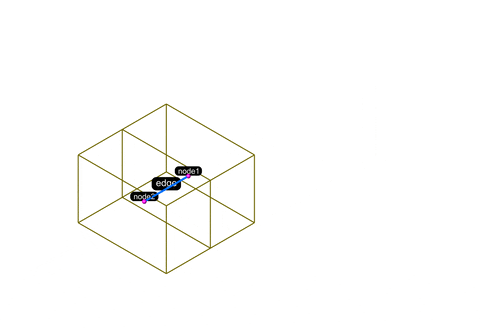Two topological cells come together to create a simple dual-graph of two nodes and one edge.

GRASSHOPPER WORKFLOW

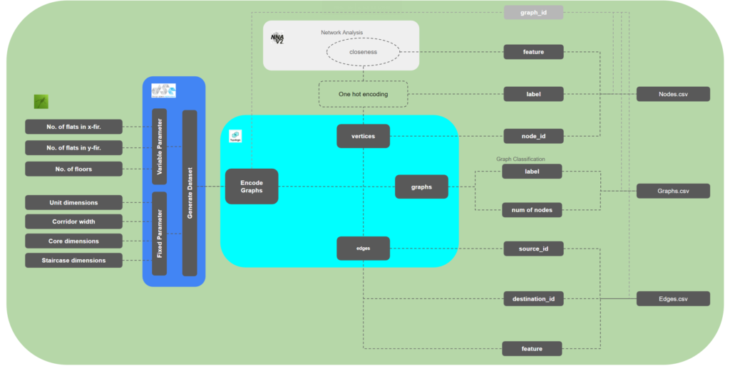
DATASET CREATION

1.Perimeter Block

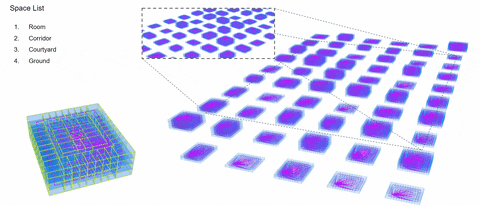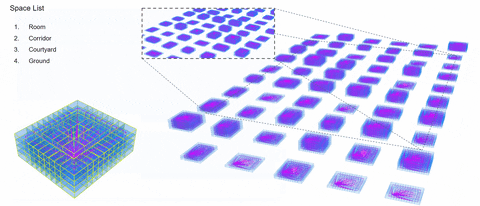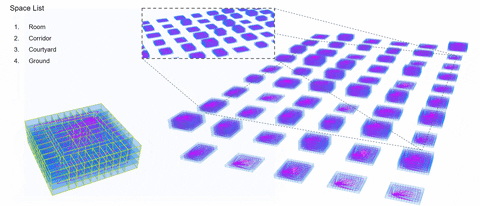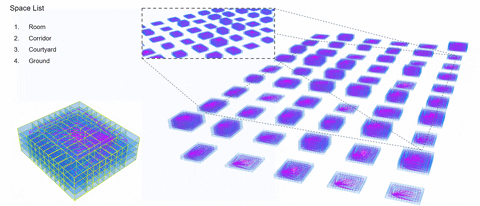
2. High-Rise Tower

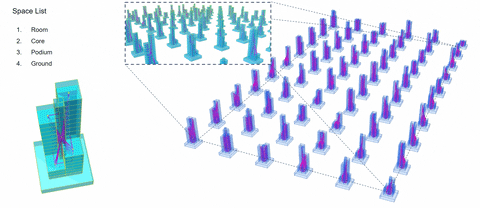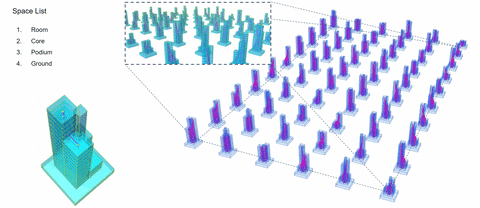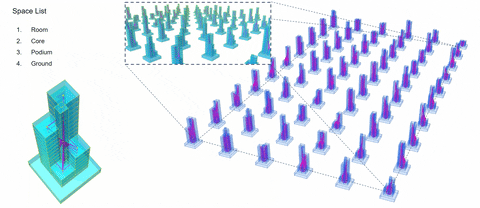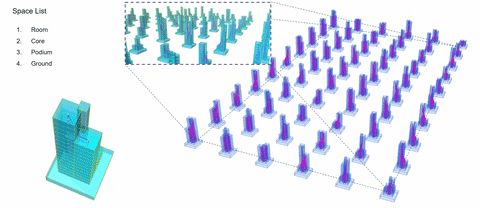
3. Slab Building

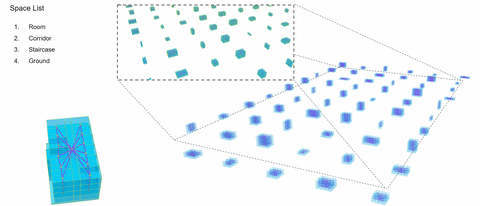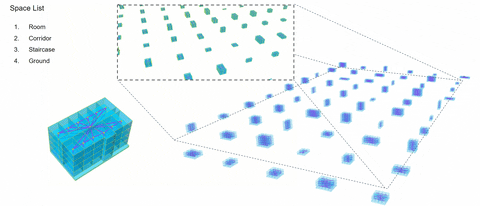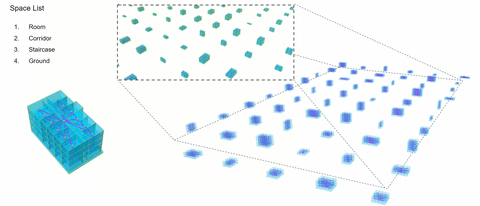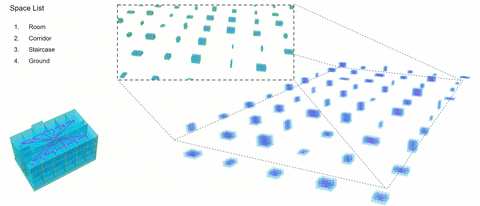
One-Hot Encoding

Node Embedding

Closeness Centrality

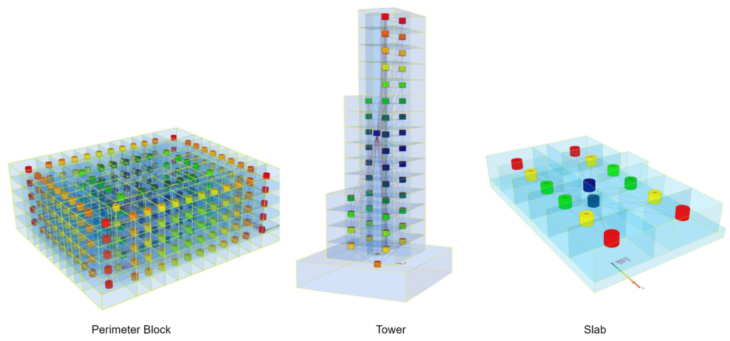
FINAL DATASET

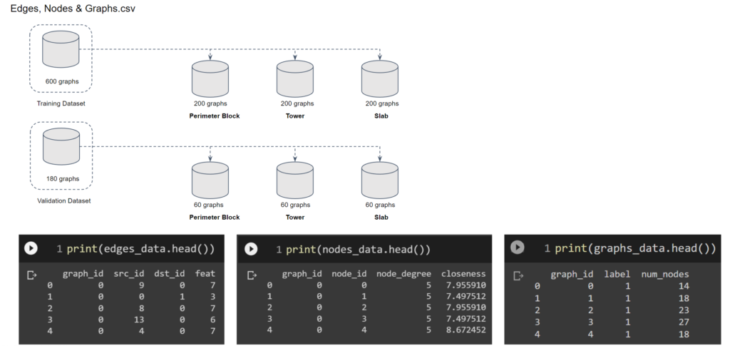
MACHINE LEARNING

DATAFLOW

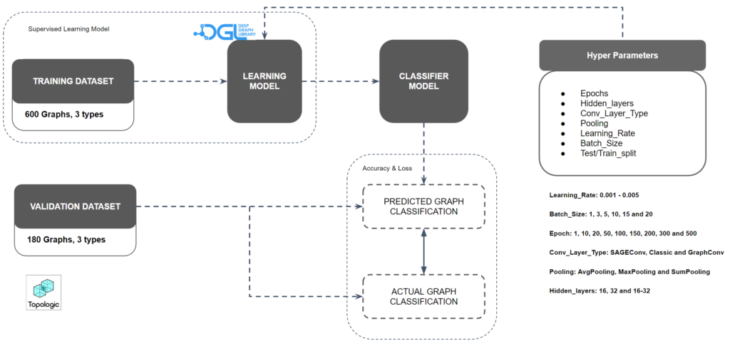
TESTING

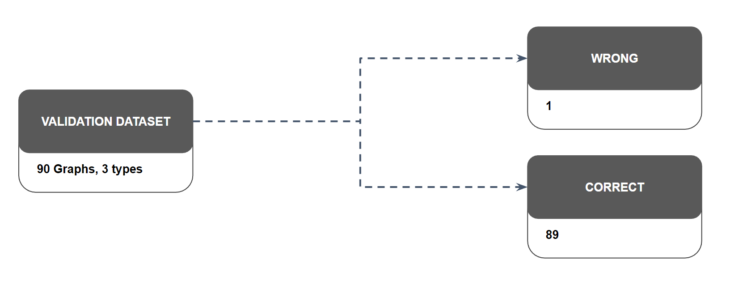
WRONG PREDICTION

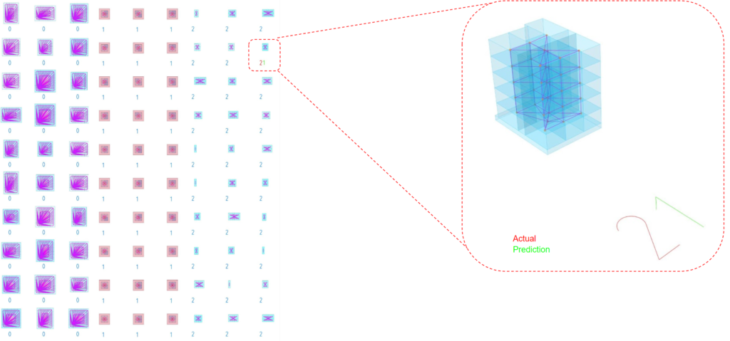
CONCLUSION

Test-1

Experimenting with batch sizes 1, 2, 3, 5, 10, 15 & 20

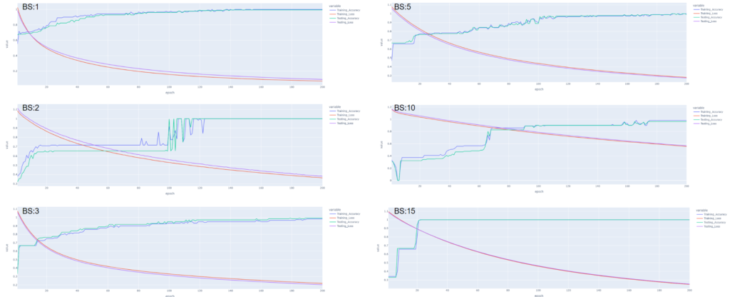
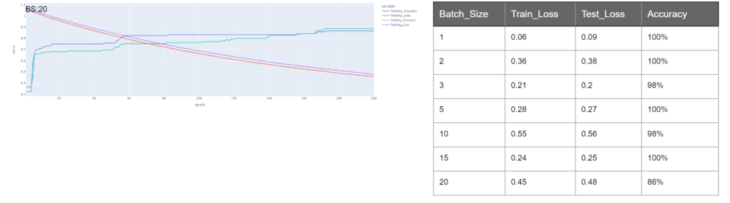
Testing through different batch sizes showed that loss increased as the batch_size also increased whereas accuracy decreased.

Test-2

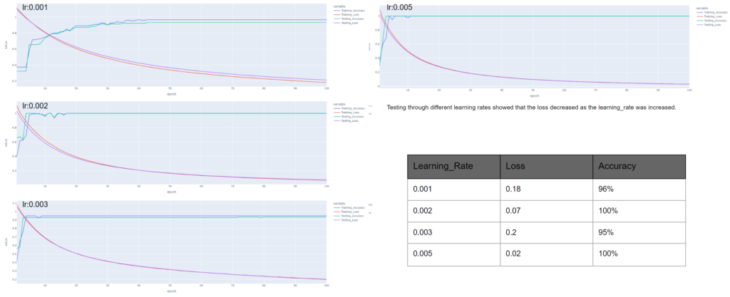
Experimenting with learning_rate: 0.001, 0.002, 0.003, and 0.005

Test-3

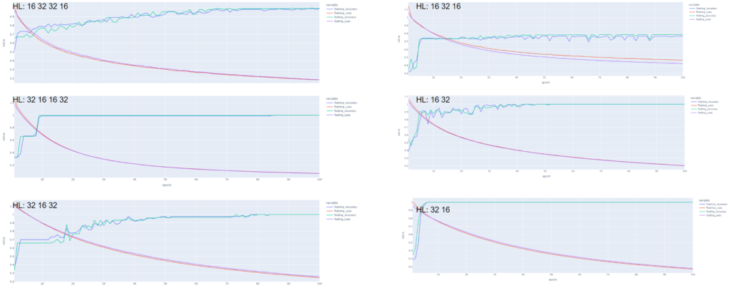
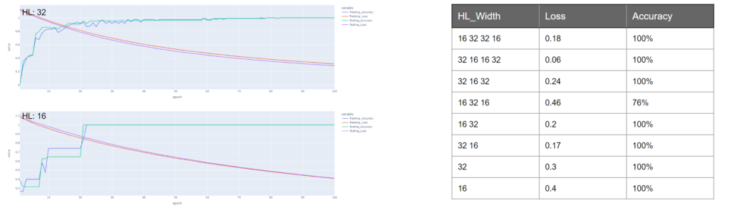
Experimenting with hidden_layer_width: 0.001, 0.002, 0.003 and 0.005

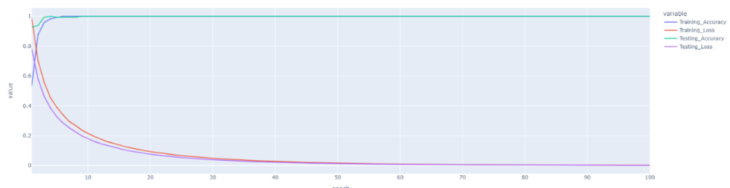
Batch_size = 20, Hidden_layers = 16, Optimizer = Adam, Epochs = 100, Conv_layer_type = SAGEConv, Learning_rate = 0.004, Loss_function = Cross_Entropy, Pooling = AvgPooling, Test/Train split = 0.2/0.8

 

Batch_size = 20, Hidden_layers = 16, Optimizer = Adam, Epochs = 500, Conv_layer_type = Classic, Learning_rate = 0.002, Loss_function = Cross_Entropy, Pooling = AvgPooling, Test/Train split = 0.2/0.8

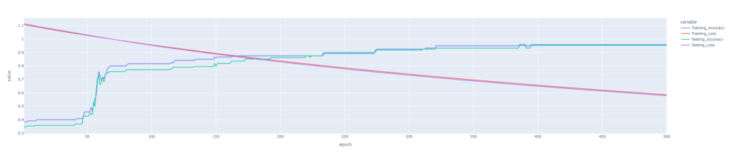
First _training_model ran for 500 epochs with a learning_rate of 0.002, batch_size 20, convolution_layer_type-> classic, one hidden layer with 16 channels, optimizer ‘adam’, avgPooling and loss_function as binary cross entropy gave learning_accuracy of 95% with a loss of 0.5

Second_training_model ran for 100 epochs with a learning_rate of 0.004, batch_size 20, convolution_layer_type-> SAGEConv, one hidden layer with 16 channels, optimizer ‘adam’, avgPooling and loss_function as binary cross entropy gave learning_accuracy of 96% with a loss of 0.2

Third_training_model also ran for 100 epochs with a learning_rate of 0.002, batch_size 1, convolution_layer_type-> SAGEConv, four hidden layer with 16 32 32 16 channels, optimizer ‘adam’, avgPooling and loss_function as binary cross entropy gave learning_accuracy of 100% with a loss of 0.001

ACKNOWLEDGEMENT

A super thank you to my guide Oana Taut and prof. David Andres Leon for their support, motivation and guidance.

I would also like to thank Dr. Wassim Jabi from Cardiff University and director of Topologic for their technical support on using Graph ML on the platform of Topologic.

A big thank you to my friend and senior Varun Mehta (IAAC alumni) for giving moral support.

REFERENCES

  1. Alexander, C., Ishikawa, S., & Silverstein, M. (1977). A pattern language : towns, buildings, construction. Oxford University Press.

  2. https://en.wikipedia.org/wiki/Spatial_network

  3. Eisenman, P. (2001). Diagram diaries. Thames and Hudson

  4. https://www.researchgate.net/publication/327891111_Topologic_tools_to_explore_architectural_topology

  5. https://www.researchgate.net/publication/344306601_Machine_Learning_Methods_for_Clustering_Architectural_Precedents_Classifying_the_relationship_between_building_and_ground

  6. https://www.researchgate.net/publication/361811023_Classifying_Building_and_Ground_Relationships_Using_Unsupervised_Graph-Level_Representation_Learning

  7. https://distill.pub/2021/gnn-intro/

  8. https://www.researchgate.net/publication/327891111_Topologic_tools_to_explore_architectural_topology

  9. https://www.researchgate.net/publication/341522458_Graph_Machine_Learning_using_3D_Topological_Models

  10. Gorny, R. A. (2019). Lecture; On Types and Typology: A critique of typological thinking

  11. https://doi.org/10.1002/ad.2406

  12. Allen, S. (2015). Field Conditions (1997). In The Digital Turn in Architecture 1992–2012, M. Carpo (Ed.).doi:10.1002/9781118795811.ch5
  13. Veloso, P., Rhee, J., & Krishnamurti, R. (2019). Multi-agent Space Planning A literature review (2008-2017)

PROJECT CREDITS

Configurable Topologies is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Master in Advanced Computation for Architecture & Design (MaCAD) 2021/22 by student Naitik Sharma under the guidance of the faculty Oana Taut.