Research Background
What is Fourier transform?
Fourier transform
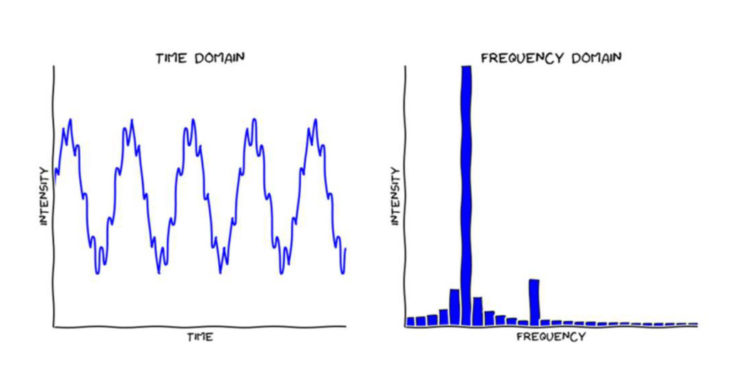
At a high level the Fourier transform is a mathematical function which transforms a signal from the time domain to the frequency domain. This is a very powerful transformation which gives us the ability to understand the frequencies inside a signal.
The Fourier Transform is used in a wide range of applications, such as image analysis, image filtering, image reconstruction and image compression.
Fourier transform in 2D(Image)

2D Fourier transform
Fourier transform is an incredibly useful tool for the analysis and manipulation of sounds and images. For images, it’s the mathematical machinery behind image compression (such as the JPEG format), filtering images and reducing blurring and noise.
Fast Fourier transform
Fast Fourier transform
The FFT manages to reduce the complexity of computing, by factoring the matrix. It has been widely used in our modern life technologies, such as wireless communication and GPS.
According to the calculation requirements of the Fast Fourier transform, the number of rows and columns of the image is required to meet the nth power of 2, so we use 128*128 pixels of the image.
Data Structure of 8bit Gray Bitmap
8bit Gray Bitmap
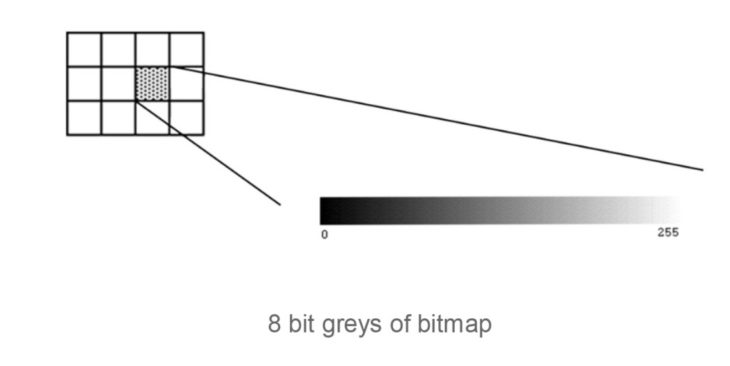
In this case each pixel takes 1 byte (8 bits) of storage resulting in 256 different states. If these states are mapped onto a ramp of greys from black to white the bitmap is referred to as a grayscale image. By convention 0 is normally black and 255 white. The grey levels are the numbers in between.
Research Goal
Research Goal
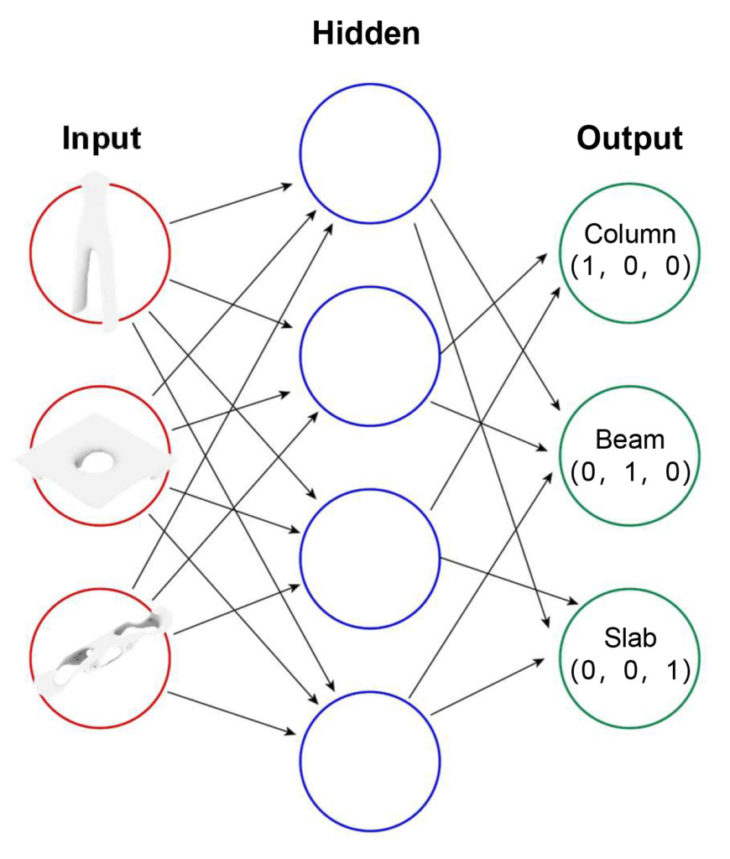
The goal of this research is trying to train the computer to recognize a complex form building element as human with neural network.
State of tha Art
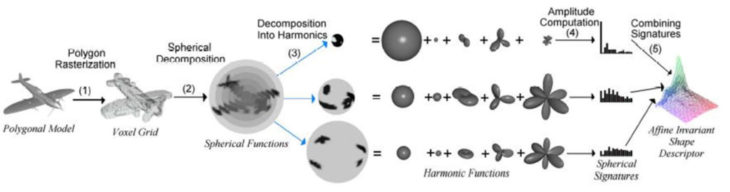
State of the Art
This is a project developed by Autodesk and Apache Kafka. The goal of this project it to train the computer to rogonize a complex geometry with ANN. In this project, they first voxelated the geometry, and then apply spherical functions to extract the signature of the geometry. Althougth the method to process the geometry can ensure the signature precisely reflect the feature of the geometry, it is still time-consuming. Insteal of voxelated the geometry, maybe there is a method that just by pixelateding the geometry, but still can extarct the signature from the data. Our research is trying to develop such a method comparatively simple.
Data Process
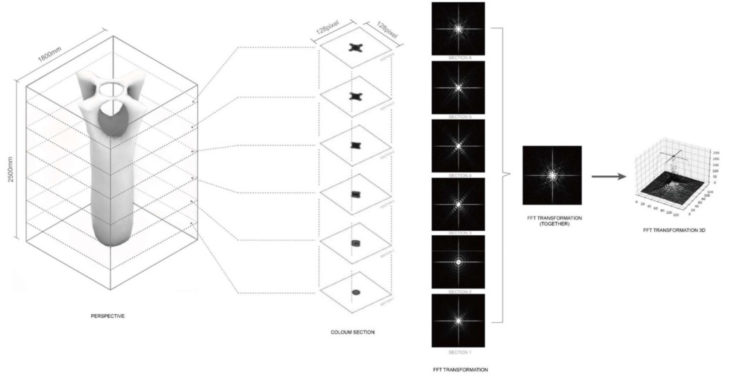
Geometry Data Process
First slice the geometry into different layers, the image size of each layer is 128 *128 pixel. The area with solid geometry will be black, the empty area will be white. Secondly, apply FFT to each image and the transform images will be generated. For those transformed images, each pixel store a integer number range from 0-255, merge these values correspondingly and later ramap the sum into range 0-255 again. Lastly, Generate a new bitmap based on the sum value per pixel, this new bitmap will be the bitmap that preserve the feature of the geometry, and will be used for ANN train later.
Here show the data process result for different building elements.
Column:
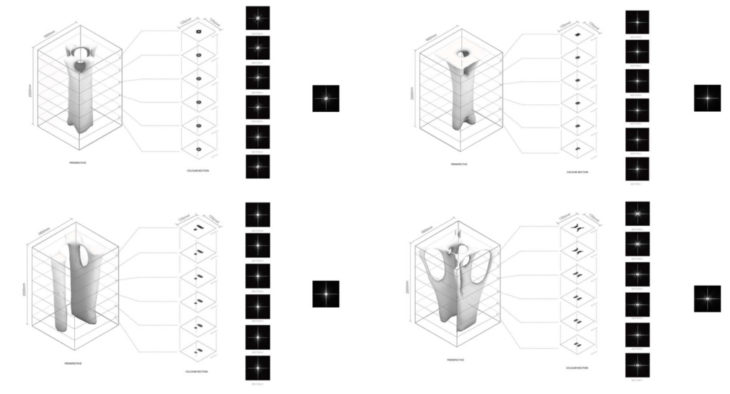
Column Result
Beam:

Beam Result
Slab:

Slab Result
ANN Set-up
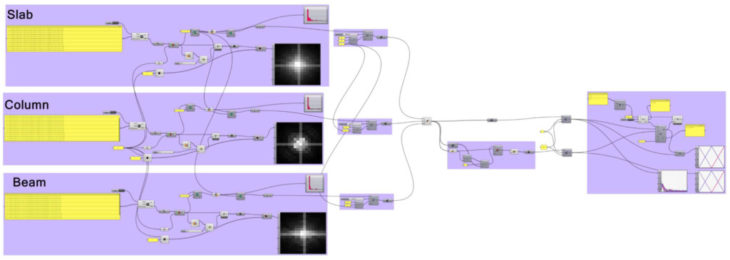
GH Code for Training
The code shows the workflow for tarining the computer to regonize the complxe geometry.
Neural Network Refine
In the train process, some problems appear because of the set-up of the neural network.

Input Layers
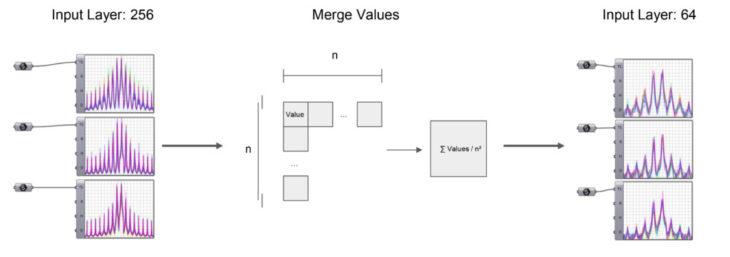
In the first try, the input layer number of the neural network is 256, which will take a lot of time to finish the tarin process. So, in order to reduce the train time, we tried to optimize the set-up of the neural network by reducing the input layers number.
Optimization Process
Input Layers
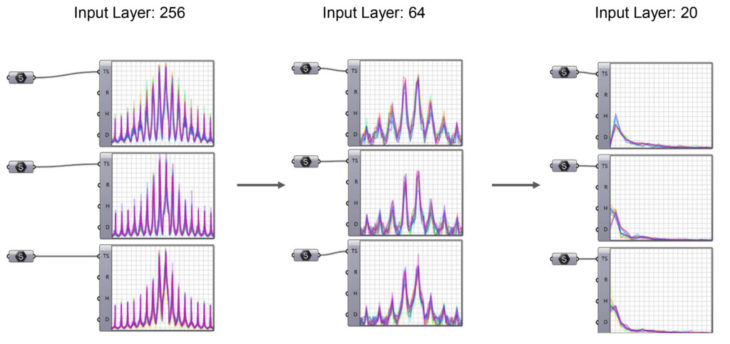
The first try is to reduce the size of the bitmap by merging the values of several pixels. And the training time doesn’t reduce a lot. And keep reducing resolution doesn’t look like a good choose, because this will lose the feature of different geometry.
So instead of reduceing the resolution of the input bitmap, we can extract the signture by another method. Because each pixel store a integer value represent the color, and this values is range from 0-255, we can divide the whole domain into 20 different domains, can count how many pixels are in certain domain. Instead of inputting the values of each pixel, we input the result of the distribution of those values. This can greatly reduce the input layers but still precisely preserve the feature of the geometry.

Input Layers
And after traning, we test the neural network will sevral sample, and the result shows high correctness of the network.

Result
Complex Geometry Identify with ANN is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Master in Advanced Architecture 2021/22 in the Business Innovation Seminar by Students: Liang Mayuqi, Jiaqi Sun, Xingyu Zhang and Ziying Zeng Faculty: Mateusz Zwierzycki