Intent
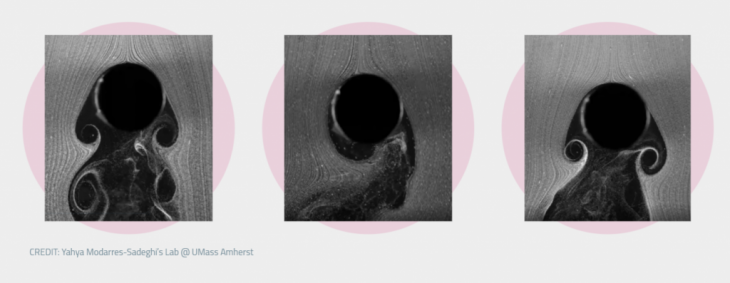
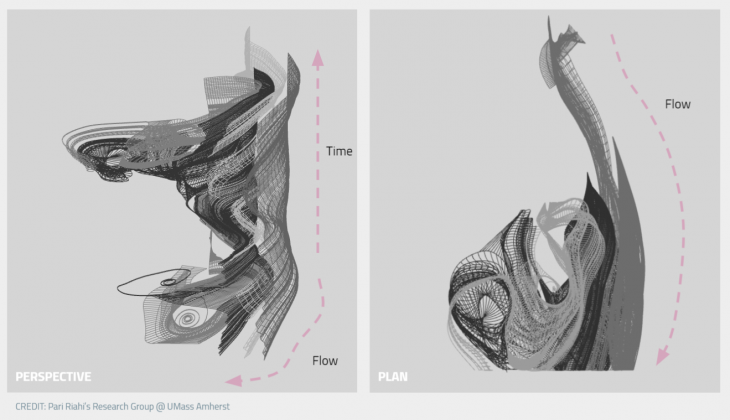
The geometric optimization project is set out to bridge the gap between complex digital models created in Rhino3D and the physical space. This provides a framework in which we can develop and prototype workflows and scaled models that allow us to design complex geometries in a feasible and economically accessible way. This specific question has been a subject of discussion on an ongoing research project that focuses on the analysis of fluid dynamic phenomena and their translation into architectural drawings and models. Collecting data from prof. Modarres-Sadeghi’s lab at UMass Amherst, a research group headed by prof. Riahi at the same institution mapped the phenomena, extrapolating time in the Z-direction, using tools such as Grasshopper and MATLAB code. This project is an exploration on how these ethereal and beautiful digital models could be converted into physical objects.
Considering the complexity of each surface, how can we build them in a way that they structurally support one another ? It is likely that each sheet on their own would topple, but could they support one another and provide entry points to experience the interstitial spaces between each of them?
APPROACH
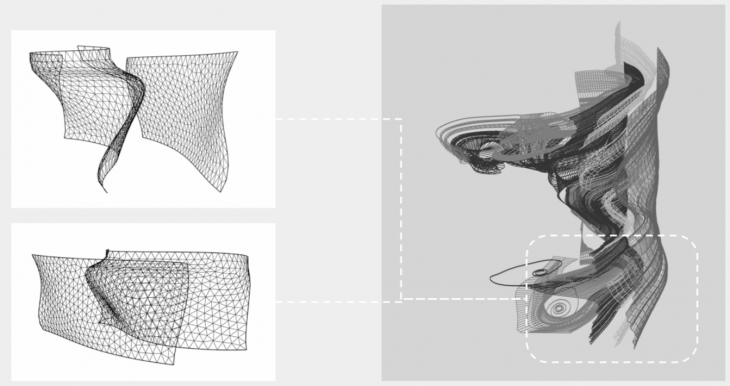
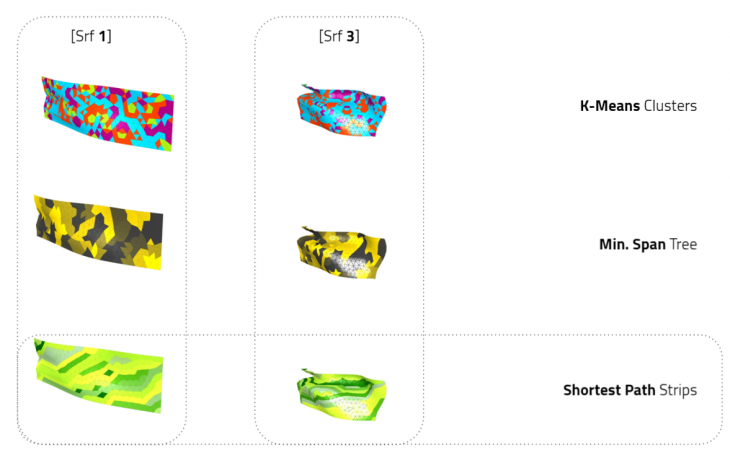
In order to explore this question, a simplified section of the model was selected, where instead of multiple sheets only two would be built to interact with one another. The first order of business was to extract the sheets, and then triangulate the mesh so we could apply the algorithms developed in class. Each sheet was put through three different algorithms, – Kmeans clustering, Minimum Spanning Trees, and Shortest Path. Kmeans showed multiple islands, most likely due to the way in which the clusters were programmed. Minimum Spanning trees showed a very nice method of clustering, and finally the shortest path strips showed some islands, but overall seemed like an approach that matched the fluidity of the studied subject.
TRY 1 & 2
Our first attempt showed issues from the beginning. The scaling method used was off, and generated overlapping tabs that felt oversized and awkward. When trying to build the model it was clear that this would not be successful. For the second try we enlarged the object, printing around 30 strips per layer and coding them with numbers. Once the printing sheet was set up, it was time to build the model. The sheets took hours to complete, and in retrospect it would have been nice to access a laser cutter or to select the Minimum Spanning Tree method rather than the strips. However, the choice of a hot glue gun improved the drying time for each strip and accelerated the building process.

THE MODEL
The final model showcases two sheets, leaning on a single section and staying standing. The bend on the internal sheet is what provides most of the support, while the exterior sheet acts as an exoskeleton. The exterior sheet, with its triangulated sections and colored strips, shows the translation from triangulated mesh to physical model, while the second image shows the scalloped effect of the tabs.

‘Algorithmic Optimization for Complex Forms’ is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Masters of Advanced Computation for Architecture & Design 2020/21 by Students: Cami Quinteros and Marissa Ridzuan and Faculty: David Leon & Dai Kandil