ACOUSTIC WALL GENERATION
The goal of the project is to predict wall configuration of variable extrusion tiles based on acoustic criteria including Reverberation time and Definition (D50) without the need of iterative analysis. Using machine learning for this problem enables short-circuiting the path between conceptual design and acoustically optimized wall.

The two desired acoustic values to predict are:
Acoustic 1: Definition or D50 – When background noise is not disturbing, the subjective speech intelligibility is often described by Definition, denoted by D50, defined as the ratio of the early received sound energy (0-50 ms after direct sound arrival) to the total received energy Source: www.akutek.info/research_files/speech_acoustics
Acoustic 2: Avg. Reverberation Time – Recommended by WHO = 0.6, defined as the time in seconds required for the level of the sound to drop 30 dB (in this calculation) after the sound source is turned off. Source: acousticbulletin.com/room-acoustic-descriptors-rt-c50-and-gain
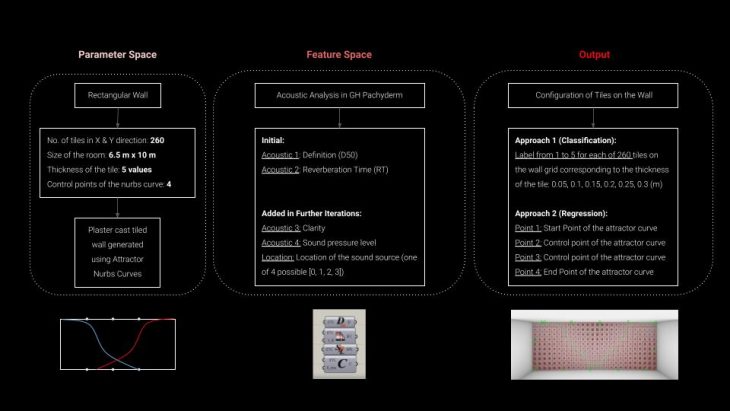
// INPUT, OUTPUT, PARAMETER SPACE
The parameter space is a rectangular wall with 260 tiles, 6.5m x 10m wall. The size of the room is based on a typical classroom size. The thickness of the tile at a given point on the wall grid is controlled by the proximity to two attractor curves and varies between 5 possible thickness values.
For the feature space, Pachyderm plug-in for Rhino and Grasshopper is used. The initial iteration was based on the Definition and Reverberation time, but we have further added Clarity (C80), Sound Pressure Level as well as we included variable location of the sound source within the room.
The output is a tiled wall. The first considered approach was classification that label 260 tiles from 1-5 based on 5 fixed values.
The second approach was to find the 4 points that are defining the attractor curve that then gets mirrored and tile thickness is controlled by the proximity to the curve.
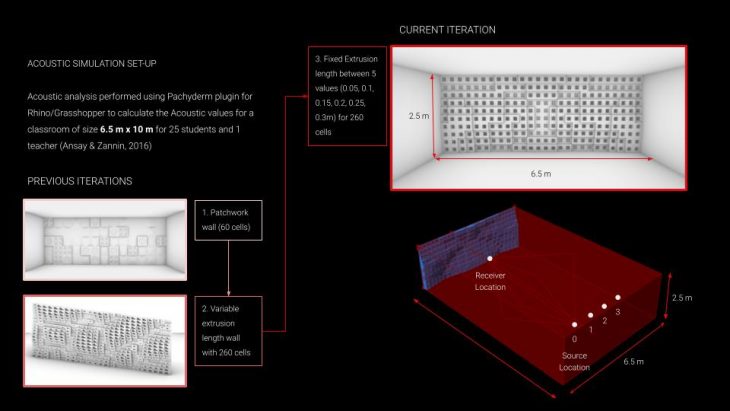
//DATASET CREATION
The first iteration of creating a dataset was based on a patchwork wall. Second was a variable extrusion wall, where thickness of the tile can vary within a continuous domain. The final set-up consist of a fixed extrusion wall, where tile thickness vary between 0.05, 0.1, 0.15, 0.2, 0.25, and 0.3m. For every wall configuration, 4 different locations of the sound source are tested and result of the acoustic analysis are saved in a csv file along with the thickness of each tile as well as location of 4 attractor curve control points.

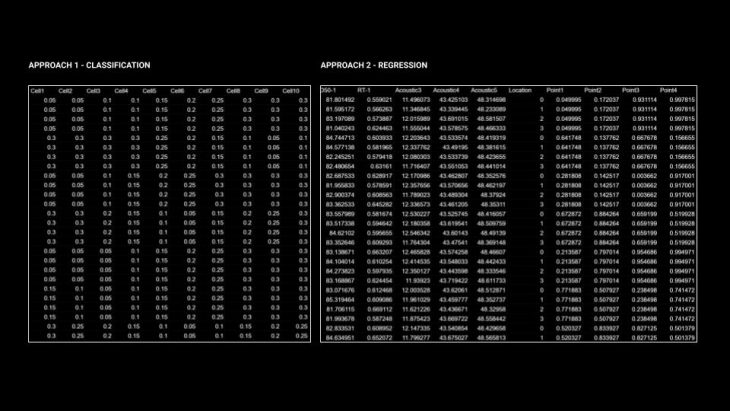
The image below shows a subset of the created dataset.
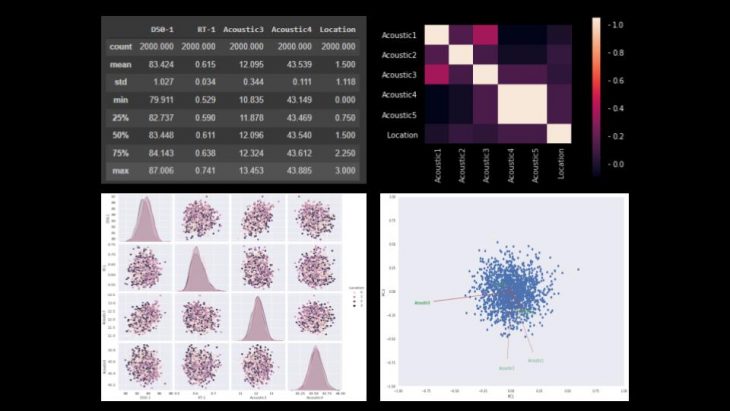
//PCA
Based on the principal component analysis, Acoustic5 value was excluded from the trainings as it appeared highly correlated to Acoustic4.
//CLASSIFICATION
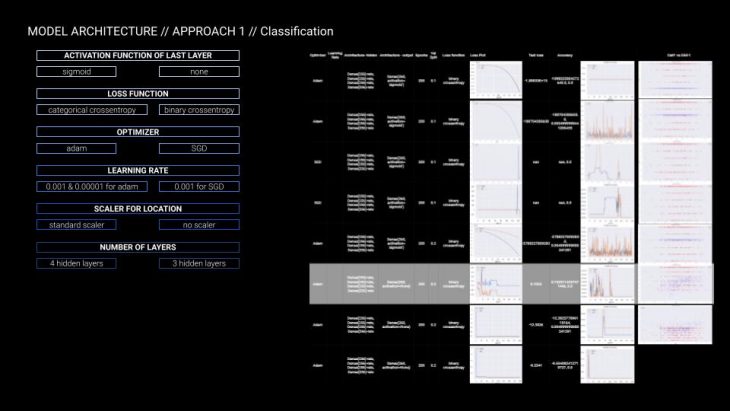
The first trial was classification with artificial neural networks. Keras Sequential model with 3 hidden layers was used. Multiple iterations were performed including variable activation functions of the last layer, loss functions, optimizers, learning rate, scalers and model architecture. The following images show model architecture as well as a subset of the iteration table with hyperparameters and plots. As the loss and accuracy diagrams did not show promising result, in the interest of time it was decided to focus on the problem as regression, predicting the position of attractor curve control points.

//REGRESSION
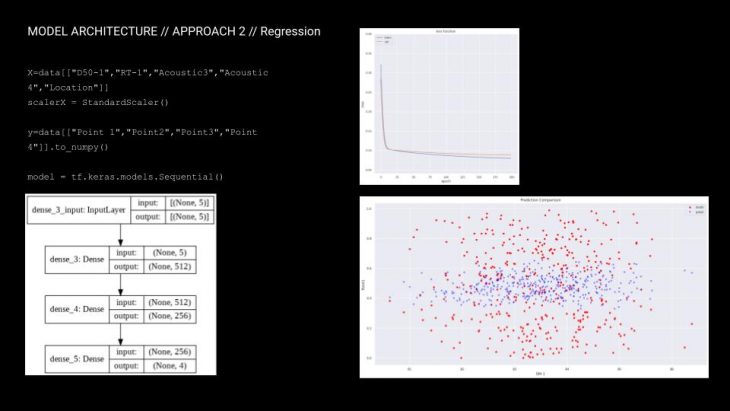
The second approach was to use regression. The model used was again keras sequential, this time with 2 hidden layers. Regression problem was tried in multiple iterations with varying hyperparameters, analogically to the classification problem. Rephrasing the problem as regression resulted in better training as observed by the loss and accuracy diagrams. However, comparing the ground truth to the predictions on the test set, averaging trend can be observed, especially for the models that resulted in the lowest test loss.

//PREDICTION IN GRASSHOPPER
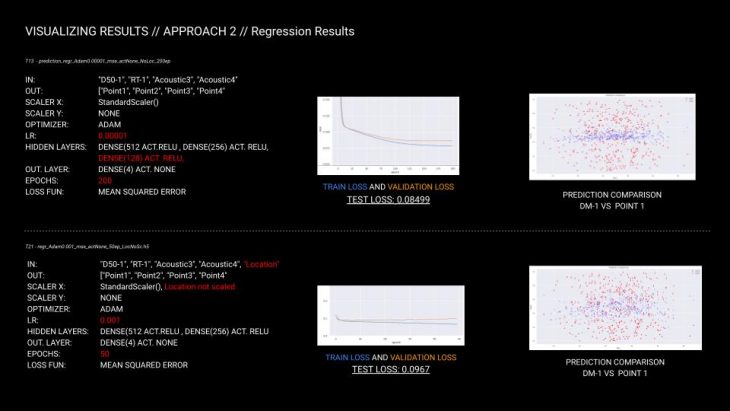
Two models were chosen for further comparison, one with the lowest test loss as well as one with less pronounced averaging trend in predictions/ground truth plot. The 2 models and corresponding scalers were saved into h5 and pickle file and used to run prediction in grasshopper using Hops component.
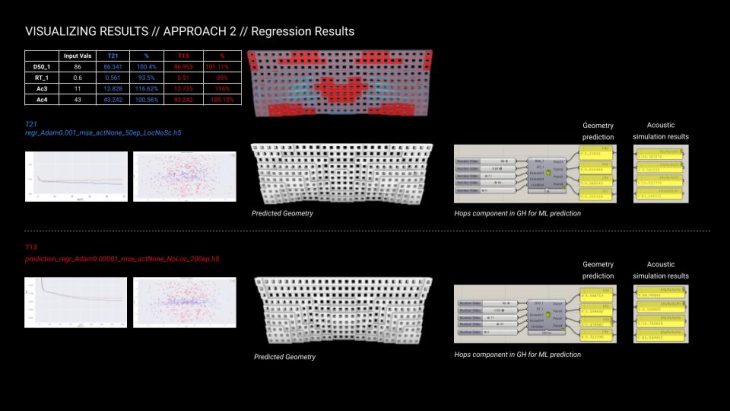
The following image presents the geometry rebuilt in grasshopper using predicted values of 4 control points of the attractor curve using both models. The input values included desired Definition (86) and Reverberation time (0.6). Acoustic analysis was run for the generated geometries to verify the accuracy of the prediction. The table shows comparison between the desired acoustic values and the result of the acoustic simulation. Predictions appeared to be quite accurate in terms of the definition value and the reverberation time, 15% difference in the values can be observed.
//CONCLUSIONS
The failure of the classification approach as well as averaging the prediction in the case of the regression approach might be due to the way the relationship between X and Y is set up . After inspection of the dataset, many of the same wall configurations provided similar acoustic results, which is to be expected owing to the nature of acoustical analysis. Additionally, the stochastic nature of acoustic simulations should be considered assuming a certain precision threshold.
Moving forward, further iterations with acoustically informed geometries and materials would be worth investigating. Another iteration with a larger dataset with greater variation in values would also provide for a more diverse model that could take into account different room types with corresponding acoustic metric targets.
//BIBLIOGRAPHY
Ansay, S., Zannin, P., Using the Parameters of Definition, D50, and Reverberation Time, RT, to Investigate the Acoustic Quality of Classrooms. Canadian Acoustics Vol. 44 No. 4 (2016)
Rossi, G., Walker, J., Sondergaard, A., Foged, I., Pasold, A., Hilmer, J., Design to manufacture workflows of sound scattering acoustic brick walls. ACADIA 2020
Fidencio, V., Moret, A., Jacob, R., Measuring noise in classrooms: a systematic review. CoDAS 2014
//CREDITS
Acoustic Wall Generation is a project of IAAC, Institute for Advanced Architecture of Catalonia developed in the Master in Advanced Computation for Architecture & Design in 2020/21 by:
Students: Aleksandra Jastrz?bska, Sumer Matharu Faculty: Gabriella Rossi, Illiana Papadopoulou