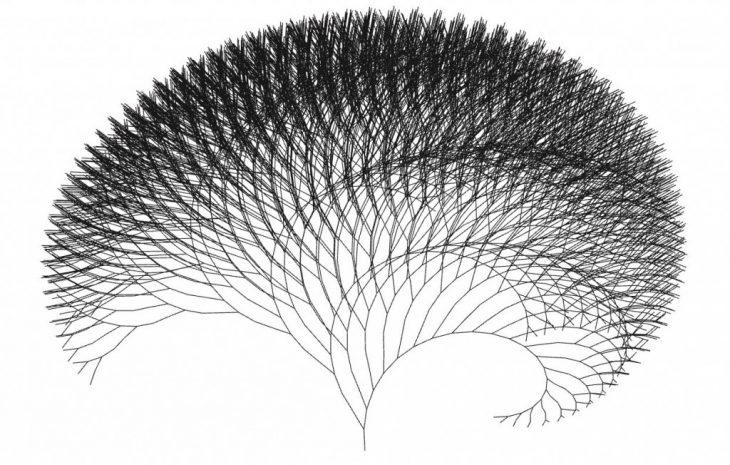
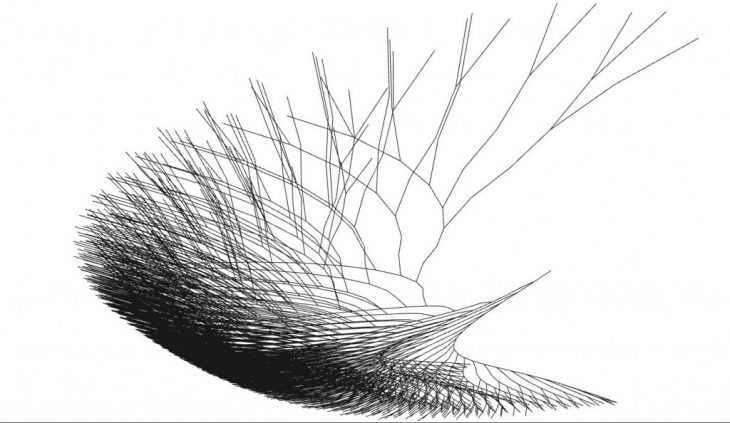
Fractal geometries can be found in almost all natural structures from mountain ranges, to wave patterns and seashells but almost nowhere are they as apparent as in bifurcation patterns such as the branching of trees, street layouts, river estuaries, blood vessels in living organisms or even the pathways of electrical arcs. These natural patterns exhibit a high (theoretically infinite) degrees of detail and complexity which allows every one of their instances to be unique in its exact shape. Simple rules governing the behavior of a particular system, paired with randomness (or infinite number of possible outcomes) generated by causality, gives rise to recursive patterns throughout ever-smaller scales of resolution and creates the properties of reality which we describe as roughness, self-similarity, periodic rhythms or symmetry. A system is said to have ‘fractal properties’ or a ‘scale free structure if a certain pattern is repeated throughout the various scales of its components.
This principle of repetition makes it possible for a vast array of complex, adaptive systems to emerge from a set of generic parameters. This concept is fundamentally different from that of euclidean geometry which is based on the abstract mathematical idea of perfectly smooth shapes with no ‘roughness’ (infinite detail) to their constituent segmenets or surfaces. The discovery of fractals therefore bridged the gap between our mathematical (exact, abstracrt, finite) understanding of the world and what we can observe in reality (variation, roughness, complexity, apparent chaos).

In the case of branching structures, initial bifurcation rules (length of segments before branching node, number, angle and direction of bifurcations) are applied repeatedly to form a self-similar, or scale invariant pattern which, theoretically, could continue through an infinite number of iterations. This concept is known as a L-system, so named after the Hungarian theoretical biologist Astrid Lindenmayer who first described its mathematical principle in 1968.

Another natural example of this logic besides the bifurcation patterns in plants, is the intricate system of blood vessels withing living creatures. From major veins and arteries to the smallest capillaries, the network of vessels in a certain organism seem to follow the same bifurcation pattern and can therefore be considered to have fractal properties. In terms of growth, regeneration and reproduction, this means that DNA must only store the basic rules for the ‘rhythm’ and type of bifurcations which can then be applied by the organism to form a complex and intricate system capable of autonomous regeneration and adaptation. It is therefore not necessary for a complete and detailed ‘map’ of the vascular system (or any other tissue with similar fractal properties) to be stored in the genetic code of an organism. This phenomenon also finds a practical application in medicine since the structure or bifurcation pattern of blood vessels can be analyses through Magnetic Resonance Imaging (MRI). The network of blood vessels in healthy tissue will display fractal properties (i.e. a regular, scale-invariant bifurcation pattern) while pathlogical tissue such as that of tumors and cancerous cells will deviate from the self-similarity of the system as a whole.