
recursive aggregation using triangular prism base geometry with rotation every second aggregation
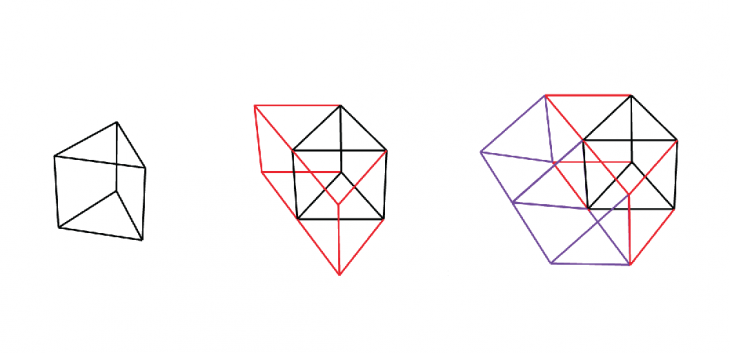
iterations: 1
objects: 5

iterations: 2
objects: 9

iterations: 3
objects: 13
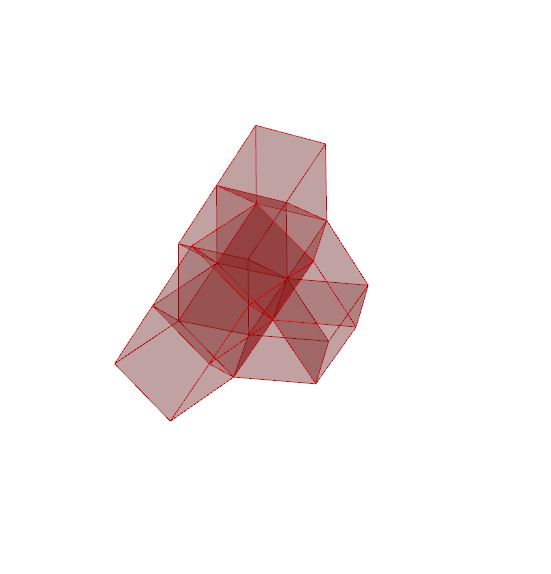
iterations: 4
objects: 21

iterations: 5
objects: 29
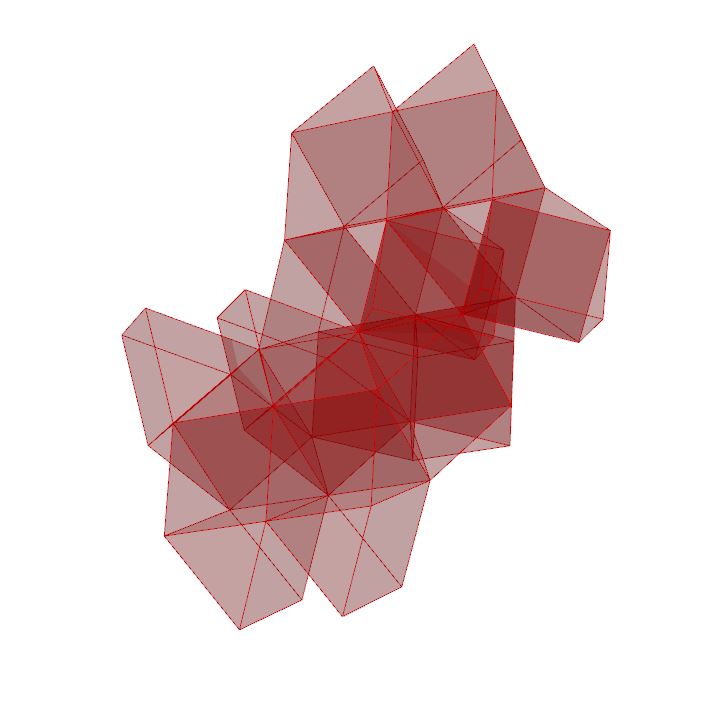
iterations: 6
objects: 45
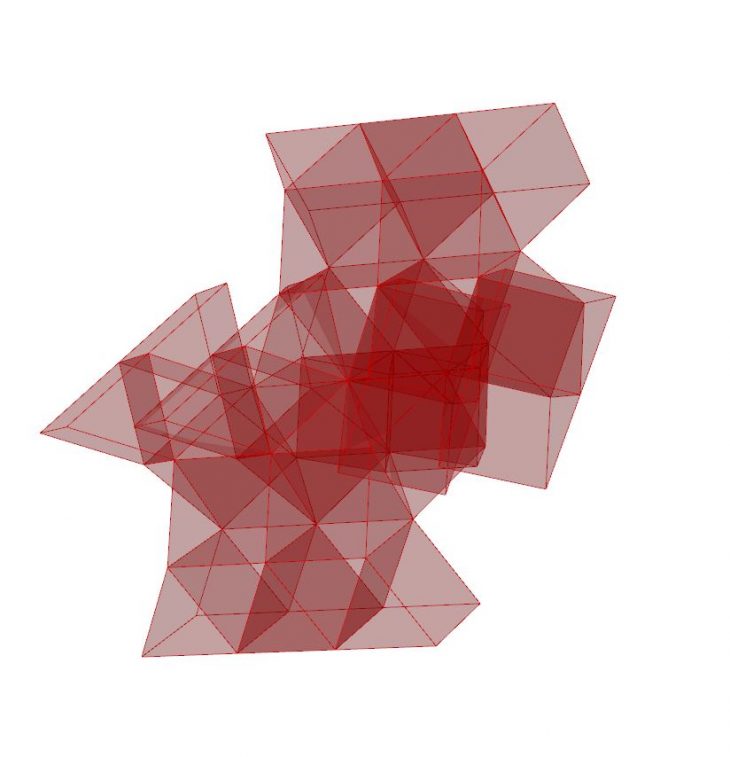
iterations: 7
objects: 61
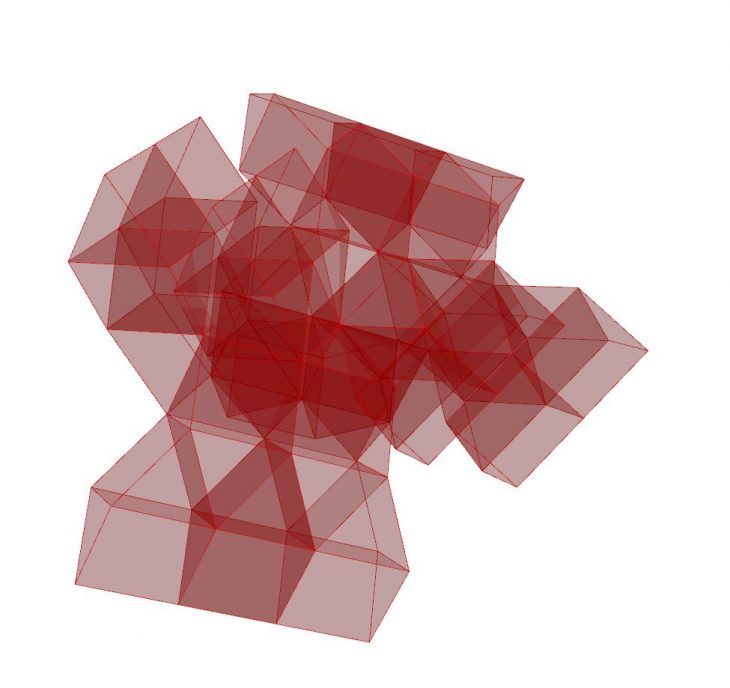
iterations: 8
objects: 93

iterations: 9
objects: 125

iterations: 10
objects: 198
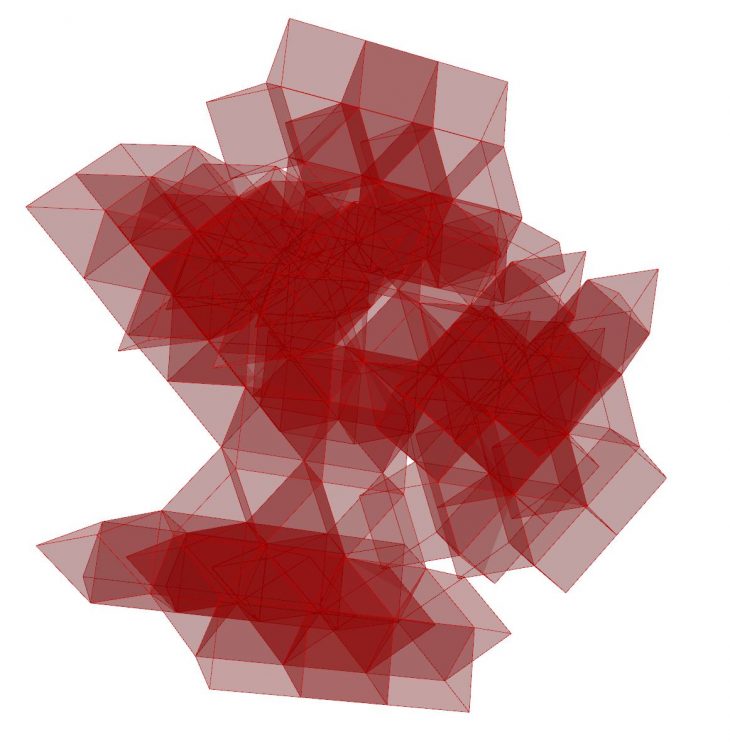
iterations: 11
objects: 253

iterations: 12
objects: 381

iterations: 13
objects: 509

iterations: 14
objects: 765

code still in work:
import rhinoscriptsyntax as rs
def allpts(srf) :
border = rs.DuplicateSurfaceBorder (srf)
lines = rs.ExplodeCurves (border)
center = rs.SurfaceAreaCentroid (srf)
allpts = []
allpts.append (center[0])
for line in lines:
pt = rs.CurveEndPoint (line)
allpts.append (pt)
return allpts
def aggregate(obj, pointList, count):
source = [pointList[0], pointList[1], pointList[2]]
target1 = [pointList[0], pointList[2], pointList[1]]
target2 = [pointList[0], pointList[3], pointList[2]]
if (count % 3 == 0):
newObject = rs.OrientObject (obj, source, target1, 1)
else:
newObject = rs.OrientObject(obj, source, target2, 1)
return newObject
def checkifduplicate(srf, newsrf):
points = allpts(srf)
newpoints = allpts(newsrf)
print points
print newpoints
print “———“
donno = 0
for newpoint in newpoints:
for point in points:
#if points[0][0]>=newpoints[0][0]-0.05 and points[0][0]<=newpoints[0][0]+0.05 and points[0][1]>=newpoints[0][1]-0.05 and points[0][1]<=newpoints[0][1]+0.05 and points[0][2]>=newpoints[0][2]-0.05 and points[0][2]<=newpoints[0][2]+0.05:
if point[0]>=newpoint[0]-0.05 and point[0]<=newpoint[0]+0.05 and point[1]>=newpoint[1]-0.05 and point[1]<=newpoint[1]+0.05 and point[2]>=newpoint[2]-0.05 and point[2]<=newpoint[2]+0.05:
print point
print newpoint
donno = donno+1
if donno == 5 or donno == 2 or donno == 1:
print “alpapalfla”
return True
return False
def checkifimhere(newObj, newObjlist):
for obj in newObjlist:
allsrf = rs.ExplodePolysurfaces(obj)
allsrfnew = rs.ExplodePolysurfaces(newObj)
for i in range(3):
for j in range(3):
for curve in rs.ExplodeCurves(rs.DuplicateSurfaceBorder(allsrfnew[i])):
if rs.CurveSurfaceIntersection(curve,allsrf[j]):
if not checkifduplicate(allsrf[j],allsrfnew[i]):
return True
return False
def recursiveAggregation(obj, gens, objList, count):
if not objList:
objList.append (obj)
allsrf = rs.ExplodePolysurfaces(obj)
pointSet1 = allpts(allsrf[0])
pointSet2 = allpts(allsrf[1])
pointSet3 = allpts(allsrf[2])
if (count % 2 == 0 and gens != 0):
newObject = aggregate(obj, pointSet1, count)
newObject2 = aggregate(obj, pointSet3, count)
objectFail = True
object2Fail = True
if (not checkifimhere(newObject,objList)):
objList.append(newObject)
objectFail = False
if (not checkifimhere(newObject2,objList)):
objList.append(newObject2)
object2Fail = False
if (gens > 0):
if not objectFail:
recursiveAggregation(newObject, gens-1, objList, count+1)
if not object2Fail:
recursiveAggregation(newObject2, gens-1, objList, count+1)
elif (gens != 0) :
newObject = aggregate(obj, pointSet2, count)
copy = rs. CopyObject(newObject)
objectFail = True
if (not checkifimhere(copy,objList)):
objList.append(copy)
objectFail = False
if (gens > 0):
if not objectFail:
recursiveAggregation(newObject, gens-1, objList, count+1)
return objList
allNewObjs = []
count = 0
a = recursiveAggregation(brep, iterations, allNewObjs, count)
My exploration in recursive aggregation with python gh began from Jose Sanchez of plethora project’s logic and further explored collision detection and variants in terms of geometrical input.
Student: Jean-Nicolas Alois Dackiw
Guest Lecturer: Long Nguyen
MRAC Faculty: Eugenio Bettucchi